Question

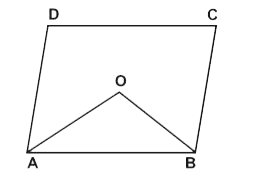
In quadrilateral ABCD, the
bisectors of $\angle A$ and $\angle B$ meet at
O and $\angle AOB={64}^{\circ }$. $\angle C+\angle D$ is equal to :
/ चतुर्भुज ABCD में, कोण A और कोण B के समद्विभाजक O पर मिलते हैं तथा $\angle AOB={64}^{\circ }$ है| $\angle C+\angle D$ का मान ज्ञात करें |

Options

A. `136^@`
B. `128^@`
C. `116^@`
D. `148^@`

Explanation

To solve the problem, we need to find the sum of angles C and D in quadrilateral ABCD, given that the angle bisectors of angles A and B meet at point O and that angle AOB is 64 degrees.

1. Understanding the Angles:
- Let angle A be denoted as \( A \) and angle B as \( B \).
- The angle bisector of angle A divides it into two equal parts, so we can denote these angles as \( X \) (for angle A) and \( Y \) (for angle B).
- Therefore, \( X = \frac{A}{2} \) and \( Y = \frac{B}{2} \).

2. Using the Triangle Property:
- In triangle AOB, we know that the sum of angles in a triangle is 180 degrees.
- Therefore, we can write the equation:
\( X + Y + \angle AOB = 180^\circ \)
- Substituting the known value of \( \angle AOB = 64^\circ \):
\( X + Y + 64^\circ = 180^\circ \)
- Rearranging gives:
\( X + Y = 180^\circ - 64^\circ = 116^\circ \)

3. Using the Quadrilateral Property:
- The sum of the interior angles of quadrilateral ABCD is 360 degrees.
- Thus, we can express this as:
\( A + B + C + D = 360^\circ \)
- Since \( A = 2X \) and \( B = 2Y \), we can substitute:
\( 2X + 2Y + C + D = 360^\circ \)
- Factoring out the 2 gives:
\( 2(X + Y) + C + D = 360^\circ \)

4. Substituting the Value of \( X + Y \):
- We already found that \( X + Y = 116^\circ \).
- Substituting this into the equation:
\( 2(116^\circ) + C + D = 360^\circ \)
- This simplifies to:
\( 232^\circ + C + D = 360^\circ \)

5. Solving for \( C + D \):
- Rearranging gives:
\( C + D = 360^\circ - 232^\circ = 128^\circ \)

Final Answer:
Therefore, the sum of angles C and D is:
\( \boxed{128^\circ} \)