In a quadrilateral ABCD, the bisectors of ∠C and ∠D meet at E. If ∠CED=56∘ and ∠A=49∘, then the measure of ∠B is:
63∘
67∘
54∘
71∘
To find the measure of angle B in quadrilateral ABCD, we will follow these steps:
Step 1: Understand the given information
We know:
- Angle CED = 56°
- Angle A = 49°
- E is the intersection of the angle bisectors of angles C and D.
Step 2: Set up the angles at point E
Let:
- Angle ECD = x
- Angle EDC = y
Since E is the intersection of the angle bisectors, we have:
- Angle C = 2x (because angle C is bisected)
- Angle D = 2y (because angle D is bisected)
Step 3: Use the triangle sum property in triangle CED
In triangle CED, the sum of the angles is 180°:
Angle ECD+Angle EDC+Angle CED=180°
Substituting the known values:
x+y+56°=180°
This simplifies to:
x+y=180°−56°=124°
Step 4: Express angles C and D in terms of x and y
From the previous step:
- Angle C = 2x
- Angle D = 2y
Step 5: Use the sum of angles in quadrilateral ABCD
The sum of the angles in a quadrilateral is 360°:
Angle A+Angle B+Angle C+Angle D=360°
Substituting the known values:
49°+Angle B+2x+2y=360°
We know from Step 3 that x+y=124°, hence 2x+2y=2×124°=248°.
Step 6: Substitute and solve for angle B
Now, substituting 2x+2y into the equation:
49°+Angle B+248°=360°
This simplifies to:
Angle B=360°−49°−248°
Calculating this gives:
Angle B=360°−297°=63°
Conclusion
Thus, the measure of angle B is 63°.
---
We know:
- Angle CED = 56°
- Angle A = 49°
- E is the intersection of the angle bisectors of angles C and D.
Let:
- Angle ECD = x
- Angle EDC = y
- Angle C = 2x (because angle C is bisected)
- Angle D = 2y (because angle D is bisected)
In triangle CED, the sum of the angles is 180°:
Angle ECD+Angle EDC+Angle CED=180°
Substituting the known values:
x+y+56°=180°
This simplifies to:
x+y=180°−56°=124°
From the previous step:
- Angle C = 2x
- Angle D = 2y
The sum of the angles in a quadrilateral is 360°:
Angle A+Angle B+Angle C+Angle D=360°
Substituting the known values:
49°+Angle B+2x+2y=360°
We know from Step 3 that x+y=124°, hence 2x+2y=2×124°=248°.
Now, substituting 2x+2y into the equation:
49°+Angle B+248°=360°
This simplifies to:
Angle B=360°−49°−248°
Calculating this gives:
Angle B=360°−297°=63°
Thus, the measure of angle B is 63°.
Topper's Solved these Questions
Similar Questions
The sides AB and AC of △ABC are produced to points D and E, respectively. The bisectors of ∠CBDand∠BCE meet at P. If ∠A=72∘, then the measure of ∠P is:
View SolutionIn quadrilateral ABCD, the bisectors of ∠A and ∠B meet at O and ∠AOB=64∘. ∠C+∠D is equal to :
/ चतुर्भुज ABCD में, कोण A और कोण B के समद्विभाजक O पर मिलते हैं तथा ∠AOB=64∘ है| ∠C+∠D का मान ज्ञात करें |
View Solution
Knowledge Check
The side BC of ΔABC is produced to D. The bisectors of ∠ABCand∠ABD meet at E. If AB = AC and ∠BEC=24∘. then the measure of ∠ABC is :
AA)60∘BB)72∘CC)48∘DD)66∘In the adjacent figure, the bisectors of ∠Aand∠B meet in a point P. If ∠C=100∘and∠D=60∘, find the measure of ∠APB.
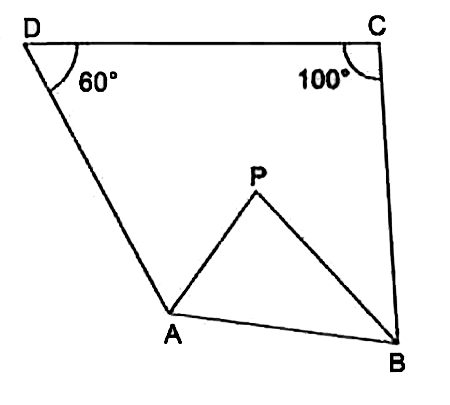 A80∘B100∘C70∘D60∘
A80∘B100∘C70∘D60∘In a quadrilateral ABCD, AO and BO are the bisectors of ∠Aand∠B respectively, ∠C=70∘and∠D=30∘. Then, ∠AOB=?
A50∘B130∘C80∘D100∘
In a △ABC, the bisectors of ∠B and ∠C meets at point O. If ∠BOC=142∘ then the measure∠A is:
△ABC में, ∠B तथा ∠C के द्विभाजक O पर मिलते हैं | यदि ∠BOC=142∘ है, तो ∠A का माप ज्ञात करे |
View SolutionΔABC ,angle B external angle C meets at P ∠A=80 then ∠BPC = ?
View SolutionIn a triagle Δ ABC, the angle bisectors of ∠ABC and ∠ACB meet at point D and angle ∠BDC is 135∘ . Find the value of ∠BAC.
View SolutionThe sides AB and AC of △ABC are produced to points D and E, respectiely. The bisectors of ∠CBD and ∠BCE meet at P. If ∠A=82∘, then the measure of ∠P is :
View SolutionABCD is a cyclic quadrilateral whose diagonals intersect at P. If AB=BC,∠DBC=70∘and∠BAC=30∘, then the measure of ∠PCD is:
View Solution
