If △ABC is a right angled triangle with ∠ABC=90∘, and AC = 10 cm and BC = 8 cm, then the length of AB is:
यदि △ABC एक समकोण त्रिभुज है, ∠ABC=90∘,AC =10, BC =8 cm फिर AB की लंबाई है:
12 cm
2 cm
18 cm
6 cm
To find the length of side AB in triangle ABC, where angle ABC is a right angle, we can use the Pythagorean theorem. The theorem states that in a right-angled triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides.
1. Identify the sides of the triangle:
- AC = 10 cm (this is the hypotenuse)
- BC = 8 cm (one of the legs)
- AB = ? (the other leg)
2. Apply the Pythagorean theorem:
The Pythagorean theorem states:
AC2=AB2+BC2
Substituting the known values:
102=AB2+82
3. Calculate the squares:
100=AB2+64
4. Rearrange the equation to solve for AB²:
AB2=100−64
AB2=36
5. Take the square root of both sides to find AB:
AB=√36
AB=6 cm
Final Answer:
The length of AB is 6 cm.
---
- AC = 10 cm (this is the hypotenuse)
- BC = 8 cm (one of the legs)
- AB = ? (the other leg)
The Pythagorean theorem states:
AC2=AB2+BC2
Substituting the known values:
102=AB2+82
100=AB2+64
AB2=100−64
AB2=36
AB=√36
AB=6 cm
The length of AB is 6 cm.
Topper's Solved these Questions
Similar Questions
Knowledge Check
ABC is a right angled triangle AB = 3 cm, BC = 5 cm and AC = 4 cm, then the inradius of the circle is :
A1 cmB1.25 cmC1.5 cmD2 cmIn a right -angled triangle ABC, ∠ABC=90∘,AB=5cm and BC = 12 cm . The radius of t he circumcircle of the triangle ABC is
A7.5 cmB6 cmC6.5 cmD7cmABC is a right angled triangle AB = 3 cm, BC = 5 cm and AC = 4 cm, then the inradius of the circle is :
 A1 cmB1.25 cmC1.5 cmDnone of these
A1 cmB1.25 cmC1.5 cmDnone of these
ABC is a right angled triangle AB = 3 cm, BC = 5 cm and AC = 4 cm, then the inradius of the circle is :

View SolutionIn a right triangle ABC ∠B=90∘ if AC=10 cm, BC=8 cm then find the length AB
View SolutionIn △ABC, AB = 6 cm, AC = 8 cm, and BC = 9 cm. The length of median AD is:
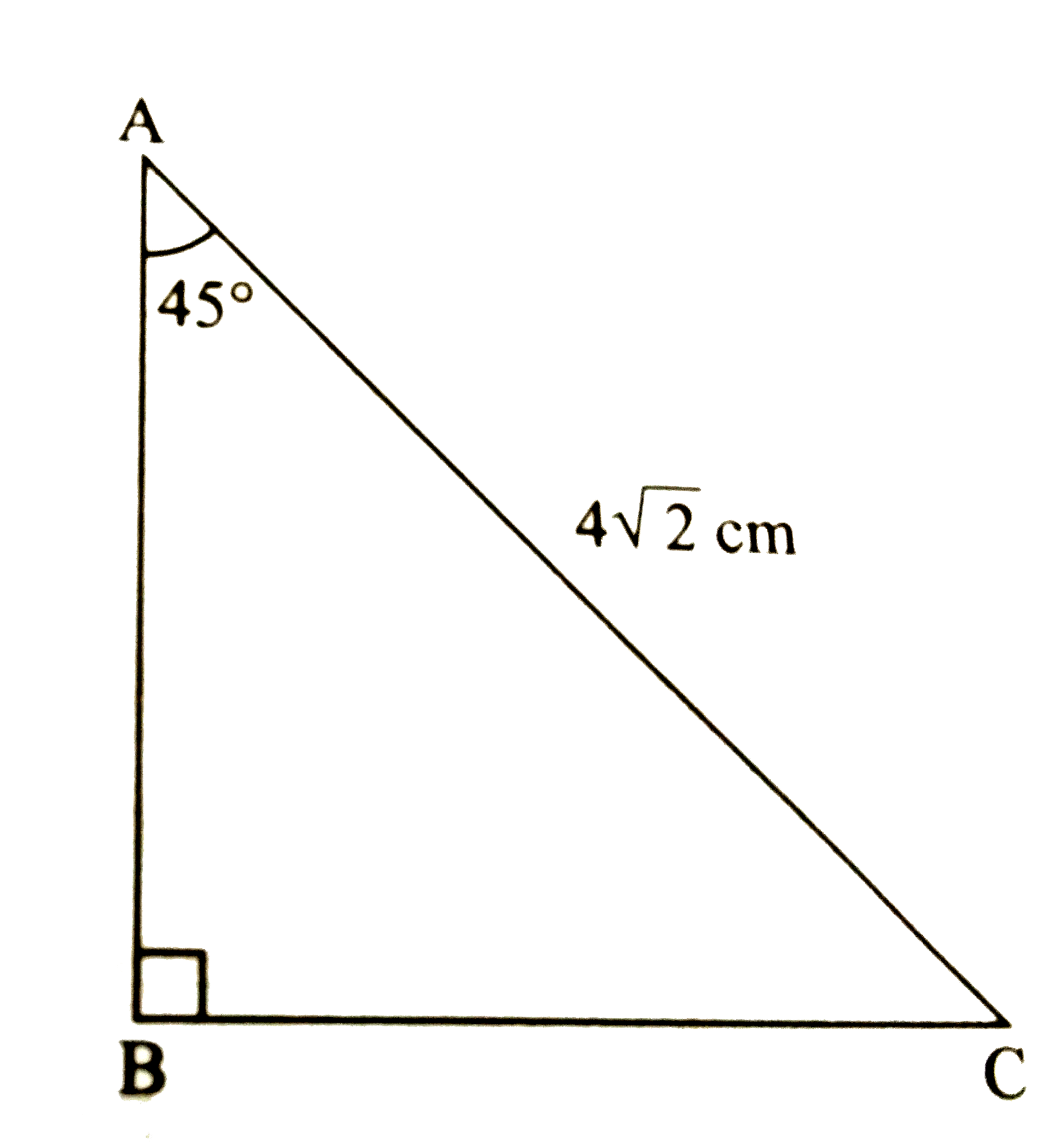
View SolutionIn △ABC,∠ABC=90∘
∠BAC=45∘ and AC =4√2cm,
then find AB.
View SolutionIn △ABC,AB=6cm,AC=8cm,andBC=9cm. The length of median AD is :
View Solution
