In a , DE is parallel to BC, AD = 3 cm, AE = 4cm and AC = 10 cm, then the value of BD in centimetres, is:
में, DE, BC & समानांतर है, AD = 3 cm, AE= 4cm और AC = 10 cm, फिर BD (सेंटीमीटर में) मान है:
3.5
7.5
4.5
5.5
To solve the problem, we will use the properties of similar triangles since DE is parallel to BC. Here are the steps:
1. Identify the Given Information:
- AD = 3 cm
- AE = 4 cm
- AC = 10 cm
- DE is parallel to BC.
2. Calculate EC:
Since AC = AE + EC, we can find EC:
EC=AC−AE=10 cm−4 cm=6 cm
3. Use the Basic Proportionality Theorem:
According to the theorem, if a line is drawn parallel to one side of a triangle, it divides the other two sides proportionally. Therefore, we have:
ADDB=AEEC
4. Substitute the Known Values:
Let DB = x. Then we can substitute the known values into the proportion:
3x=46
5. Cross-Multiply to Solve for x:
Cross-multiplying gives:
3⋅6=4⋅x
18=4x
6. Solve for x:
Divide both sides by 4:
x=184=4.5 cm
7. Conclusion:
Therefore, the value of BD is:
BD=4.5 cm
Final Answer:
BD = 4.5 cm
- AD = 3 cm
- AE = 4 cm
- AC = 10 cm
- DE is parallel to BC.
Since AC = AE + EC, we can find EC:
EC=AC−AE=10 cm−4 cm=6 cm
According to the theorem, if a line is drawn parallel to one side of a triangle, it divides the other two sides proportionally. Therefore, we have:
ADDB=AEEC
Let DB = x. Then we can substitute the known values into the proportion:
3x=46
Cross-multiplying gives:
3⋅6=4⋅x
18=4x
Divide both sides by 4:
x=184=4.5 cm
Therefore, the value of BD is:
BD=4.5 cm
BD = 4.5 cm
Topper's Solved these Questions
Similar Questions
Knowledge Check
In the figure, if DE || BC, AD = 3 cm, BD = 4 cm, and BC = 14 cm, then DE equals :
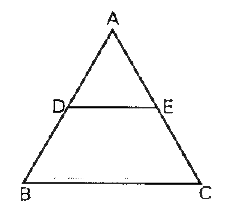 A7 cmB6 cmC4 cmD3 cm
A7 cmB6 cmC4 cmD3 cmIn triangle ABC,∠BAC=90∘and AD is perpendicular to BC. If AD=6cmand BD=4cm, then the length of BC is:
A10 cmB12 cmC13 cmD15 cm.
In △ABC ,D is a median from A to BC, AB = 6cm , AC =8cm and BC = 10cm The length of median AD (in cm ) is :
triangle ABC में, D, A से BC पर एक पर स्थित माध्यिका है।, AB = 6 सेमी, AC=8 सेमी और BC = 10 सेमी है। माध्यिका AD की लंबाई (सेमी में) है
View SolutionIn triangle ABC, ∠BAC=90∘andAD⊥BC. If BD = 3 and CD = 4 cm, then the length of AD is.
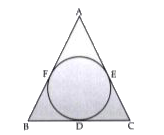
View SolutionA triangle ABC is drawn to circumscribe a circle. If AB = 13 cm, BC = 14 cm and AE =7 cm, then find AC.
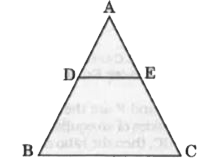
View SolutionIn figure, DE || BC. IF DE = 3 cm, BC = 6 cm and area of ΔADE=15 sq. cm, then the area of ΔABC is
View SolutionIn a △ABC, DE is parallel to BC where D and E are the points on AB and AC, respectively and AD = 4cm, DB = 8 cm, AE= 3 cm, Length of EC is:
triangle ABC में, DE, BC के समांतर है जहाँ D और E क्रमशः AB और AC पर बिंदु ह, और AD = 4 सेमी , DB= 8 सेमी , AE = 3 सेमी , तो EC की लम्बाई है ?
View SolutionIn ΔABC,DE∣∣BC so that AD==2.4cm,AE=3.2cmandEC=4.8cm, then , AB= ?
View Solution

