In △PQR,∠P=90∘, S and
T are the mid points of the sides PR and PQ, respectively. What is the value of RQ2/(QS2+RT2) ?
△PQR में, ∠P=90∘, S और T
क्रमशः PR और PQ भुजाओं के मध्य बिंदु है| RQ2/(QS2+RT2) का मान क्या है
a)34
b)12
c)23
d)45
To solve the problem, we need to find the value of RQ2QS2+RT2 in triangle PQR where ∠P=90∘, and S and T are the midpoints of sides PR and PQ respectively.
1. Identify the triangle and midpoints:
- We have triangle PQR with P at the right angle.
- Let S be the midpoint of PR and T be the midpoint of PQ.
2. Assign lengths to the sides:
- Let PQ=2a and PR=2b for some positive values a and b.
- Since S and T are midpoints, we have:
- PS=b (half of PR)
- PT=a (half of PQ)
3. Calculate RQ2:
- Using the Pythagorean theorem in triangle PQR:
RQ2=PQ2+PR2=(2a)2+(2b)2=4a2+4b2=4(a2+b2)
4. Calculate QS2:
- In triangle QPS, we apply the Pythagorean theorem:
QS2=PQ2+PS2=(2a)2+b2=4a2+b2
5. Calculate RT2:
- In triangle PRT, we again apply the Pythagorean theorem:
RT2=PR2+PT2=(2b)2+a2=4b2+a2
6. Combine QS2 and RT2:
- Now we need to calculate QS2+RT2:
QS2+RT2=(4a2+b2)+(4b2+a2)=4a2+b2+4b2+a2=5a2+5b2=5(a2+b2)
7. Calculate the ratio:
- Now we can find the value of RQ2QS2+RT2:
RQ2QS2+RT2=4(a2+b2)5(a2+b2)=45
Final Answer:
The value of RQ2QS2+RT2 is 45.
---
- We have triangle PQR with P at the right angle.
- Let S be the midpoint of PR and T be the midpoint of PQ.
- Let PQ=2a and PR=2b for some positive values a and b.
- Since S and T are midpoints, we have:
- PS=b (half of PR)
- PT=a (half of PQ)
- Using the Pythagorean theorem in triangle PQR:
RQ2=PQ2+PR2=(2a)2+(2b)2=4a2+4b2=4(a2+b2)
- In triangle QPS, we apply the Pythagorean theorem:
QS2=PQ2+PS2=(2a)2+b2=4a2+b2
- In triangle PRT, we again apply the Pythagorean theorem:
RT2=PR2+PT2=(2b)2+a2=4b2+a2
- Now we need to calculate QS2+RT2:
QS2+RT2=(4a2+b2)+(4b2+a2)=4a2+b2+4b2+a2=5a2+5b2=5(a2+b2)
- Now we can find the value of RQ2QS2+RT2:
RQ2QS2+RT2=4(a2+b2)5(a2+b2)=45
The value of RQ2QS2+RT2 is 45.
Topper's Solved these Questions
Similar Questions
In △ABC, P and Q are the middle points of the sides AB and AC respectively. R is a point on the segment PQ such that PR: RQ =1: 2. If PR = 2cm, then BC =?
△ABC में, P और Q क्रमशः भुजाओं AB तथा AC के मध्य बिंदु हैं। R, PQ पर एक बिंदु इस प्रकार है कि PR: RQ =1: 2 यदि PR=2 सेमी, तो BC=
View SolutionIn the given figure , PQR is an equilateral triangle with side as 12 cm . S and T are the mid points of the sides PQ and PR respectively . What ist he area (in cm2) of the shaded region ?
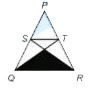
View Solution
Knowledge Check
In ΔPQR,SandT are the mid points of sides PQ and PR respectively. If ∠QPR=45∘and∠PRQ=55∘, then what is the value (in degrees) of ∠QST ?
A80B85C90D100In a square PQRS, X and Y are mid points of sides PS and QR respectively. XY and QS intersect a t O. Find the area of ΔXOS, if PQ = 8 cm.
A6 cm2B12 cm2C4 cm2D8 cm2PQR is a triangle. S and T are the midpoints of the sides PQ and PR respectively. Which of the following is TRUE?
I. Triangle PST is similar to triangle PQR.
II. ST = 1/2(QR)
III. ST is parallel to QR. / ST, QRAOnly I and IIBOnly II and IIICOnly I and IIIDAll I, II and III
In △PQR, S and T are mid-points of PQ and PR, respectively. If ∠QPR=75∘ and ∠PQR=40∘, then ∠TSQ is:
△PQR में, S और T क्रमशः PQ और PR के मध्य-बिंदु हैं, यदि ∠QPR=75∘ और ∠PQR=40∘ तो ∠TSQ है :
View SolutionIn the given figure, PQR is an equilateral triangle with side as 12cm. S and T are the mid points of the sides PQ and PR respectively. What is the area (in cm2) of the shaded region?
दी गई आकृति में PQR एक समबाहु त्रिभुज है जिसकी भुजा 12 से.मी. हैं। S तथा T क्रमशः भुजा PQ तथा PR के मध्य बिन्दु है। छायांकित भाग का क्षेत्रफल (से.मी.2 में) क्या है?
View SolutionA triangle PQR is a right angled triangle at Q. E and F are the mid points of QR and PR respectively. What will be the ratio of the area of quadrilateral PQEF to the area of triangle PQR.
एक समकोण त्रिभुज PQR, E पर समकोण है E और F क्रमशः QR और PR के मध्य बिंदु हैं। चतुर्भुज PQEF के क्षेत्रफल और त्रिभुज PQR के क्षेत्रफल का अनुपात क्या होगा
View SolutionIn a rhombus PQRS , PR and QR are the diagonals of the rhombus. If PQ=10cm, then find the value of PR2+QS2.
View SolutionIn the given, ABCDEF is a regular hexagon of side 12cm. P, Q and R are the mid points of the sides AB, CD and EF respectively. What is the area (in cm2) of triangle PQR?
दी गई आकृति में , ABCDEF एक सम षट्भुज है जिसकी भुजा 12 से.मी.? है। P, Q तथा R क्रमशः भुजाओं AB, CD तथा EF के मध्य बिन्दु है। त्रिभुज PQR का क्षेत्रफल (से.मी.2 में) क्या है?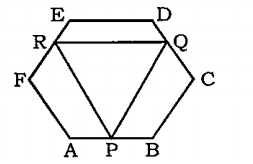
View Solution
