A stone thrown from the ground at an angle of 45∘ above the horizontal strikes a vertical wall at a point 10 m above the ground. If the wall is at a distance of 20m from the point of projection, find (take g=10ms−2)
a. the speed with which the stone is projected.
b. the magnitude and direction of the velocity of the stone when it strikes the wall.

Let P be the point on the wall where the stone strikes it. Taking the point of projection O as the origin, the coordinates of P are (20m,10m)
x=(ucosθ)t……….1
y=(usinθ)t−1tgt2.........2
putting x=20m,y=10m,g=10ms−2 and θ=45∘ in Eqs 1 and 2 we have
20=(ucos45∘)t=u√2t
⇒t=20√2u.........3
and 10=(usin45∘)t−12×10×t2
⇒10=ut√2−5t2...........4
Using 3 and 4
10=u√2×20√2u−5(20√2u)2
⇒10=20−4000u2⇒u2=400
⇒u=20ms−1
b. At point P,vx=20cos45∘=20√2ms−1
uu=usinθ=20sin45∘=20√2ms−1
v2y=u2y−2g×10⇒u2y=4002−2×10×10
⇒v2y=0⇒vy=0
Hence point P is at the highest point on the trajectory where the velocity is only horizontal. Thus thestone strikes the wall at P with a velocity of 20√2=10√2ms−1 in the horizontal direction.
Similar Questions
A projectile shot at an angle of 450 above "the horizontal strikes a building 30m away at a point 15m above the point of projection.The magnitude and direction of velocity of projectile when it strikes the building?
View SolutionA projectile shot at angles of 45∘ above the horizontal strikes a building 30 m away at a point 15 m above the point of projection. Find : (a) the speed of projection . (b) the magnitude and direction of velocity of projectile when it strikes the building .
View Solution
Knowledge Check
A stone is thrown from the top of a tower at an angle of 30∘ above the horizontal level with a velocity of 40 m/s. it strikes the ground after 5 second from the time of projection then the height of the tower is
A20 mB25 mC40 mD55mA particle just clear a wall of height b at a distance a and strikes the ground at a distance from the point of projection, the angle of projection is :
Atan−1(bac)B45∘Ctan−1(bca(c−1))Dtan−1(bca)A ball is thrown from the ground so as to just clear a wall 10m high at a distance of 20m and falls at a distance of 40m from the wall. The magnitude and direction of the projection velocity is
A10m/s,30∘B25m/s,60∘C25m/s,tan−1(3/4)D10m/s,tan−1(3/4)
A stone is thrown from the top of a tower at an angle of 30∘ above the horizontal level with a velocity of 40 m/s. it strikes the ground after 5 second from the time of projection then the height of the tower is
View SolutionA projectile shot at an angle of 45∘ above the horizontal strikes the wall of a building 30m away at a point 15m above the point of projection.Initial velocity of the projectile is?
View SolutionA ball is thrown from the ground so that it just crosses a wall 5m high at a distance of 10m and falls at a distance of 10m ahead from the wall. Find the speed and the direction of projection of ball. Assume, g=10 ms–2
View SolutionA ball is thrown from the ground so that it just crosses a wall 5m high at a distance of 10m and falls at a distance of 10m ahead from the wall. Find the speed and the direction of projection of ball. Assume, g=10 ms–2
View SolutionA particle is projected horizontally with speed u from point A, which is 10 above the ground . If the particle hits the inclined perpendicularly at point B. [ g =10m/s2]
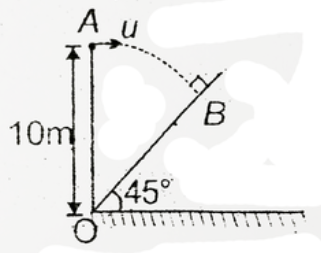
Find horizontal speed with which the particle was projected
View Solution
