A boat crosses a river from part A to part B which are just on opposite side. The speed of the water is vw and that of boat is vb relative to still water. Assume vb=2vw. What is the time taken by the boat if it was to cross the river directly on the AB line?
2Dvb√3
√3D2vb
Dvb√2
D√2vb
The correct Answer is:A
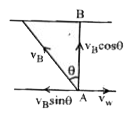
Let D be the width of river vBsinθ=vw
sinθ=vwvB=12(∴vB=2vw)⇒θ=30∘
Time taken to cross the river t=Dvbcosθ=2Dvb√3
Similar Questions

Two ports, A and B, on a north-south line ar separated by a river of width D. The river flows east with speed u. A boat crosses the river starting from port A. The speed of the boat relative to the river is v. Assume v=2u
Q. What is the direction of the velocity of boat relative to river θ, sothat it crosses directly on a line from A to B?
View SolutionA boat crosses river of width 60√7m inshortest possible path.Speed of river is 8ms and speed of the boat in , still water is 6ms .Find the time taken by boat(in seconds) to cross the river.
View Solution
Knowledge Check

Two ports, A and B, on a north-south line ar separated by a river of width D. The river flows east with speed u. A boat crosses the river starting from port A. The speed of the boat relative to the river is v. Assume v=2u
Q. What is the direction of the velocity of boat relative to river θ, sothat it crosses directly on a line from A to B?A30∘ west of northB30∘ east of northC60∘ west of northD60∘ east of northA boat crosses a river of width 1 km by shortest path in 15 min. if the speed of boat in still water is 5 kmh−1, then what is the speed of the river?
A5 kmh−1B12 kmh−1C3 kmh−1D4 kmh−1
Two ports, A and B, on a north-south line ar separated by a river of width D. The river flows east with speed u. A boat crosses the river starting from port A. The speed of the boat relative to the river is v. Assume v=2u
Q. The boat crosses the river from A to the other side in shortest possible time, then how far is the boat from the port B after crossing the riverAD√2B√2DC2DDD2

Two ports, A and B, on a north-south line ar separated by a river of width D. The river flows east with speed u. A boat crosses the river starting from port A. The speed of the boat relative to the river is v. Assume v=2u
Q. The boat crosses the river from A to the other side in shortest possible time, then how far is the boat from the port B after crossing the river
View Solution
Two ports, A and B, on a north-south line ar separated by a river of width D. The river flows east with speed u. A boat crosses the river starting from port A. The speed of the boat relative to the river is v. Assume v=2u
Q. Suppose the boat wants to cross the river from A to the other side in the shortest possible time. Then what should be the direction of the velocity of boat relative to river?
View Solution(a) In which direction should the motorboat given in Illustration 5.46 head in order to reach a point on the opposite bank directly east from the starting point ? The boat's speed relative to the water remains 4ms−1.
(b) What is the velocity of the boat relative to the earth ?
( c) How much time is required to cross the river ?
View Solution
Two ports, A and B, on a north-south line ar separated by a river of width D. The river flows east with speed u. A boat crosses the river starting from port A. The speed of the boat relative to the river is v. Assume v=2u
Q. Suppose the boat wants to cross the river from A to the other side in the shortest possible time. Then what should be the direction of the velocity of boat relative to river?
View SolutionA man in a row boat must get from point A to point B on the opposite bank of the river (see figure).The distance BC=a.The width of the river AC=b.At what minimum speed u relative to the still water should the boat travel to reach the point B?The velocity of flow of the river is v0

View Solution
