A ring is suspended from a point S on its rim as shown in figure. It behaves like a seconds pendulum. If g=π2 , The radius of the ring is
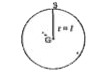
0.1 m
0.3 m
0.5 m
1.0 m
The correct Answer is:C
For a compound pendulum, T=2π√K2+l2lg (For ring r = K) because I=MK2=mr2
Here l = r = K , T = 2 sec , g=π2∴2=2π√r2+r2rg=2π√2r2rπ2 or 2=2ππ√2r=2√2r
∴√2r=1⇒2r=1 or r=12=0.5m∴ Radius of ring = 0.5 m.
Similar Questions
Knowledge Check
A ring is suspended at a point on its rim and it behaves as a second’s pendulum when it oscillates such that its centre move in its own plane. The radius of the ring would be (g = π2)
A0.5 mB1.0 mC0.67 mD1.5 mThe ring B is coaxial with a solenoid A as shown in figure. As the switch S is closed at t=0, the ring B
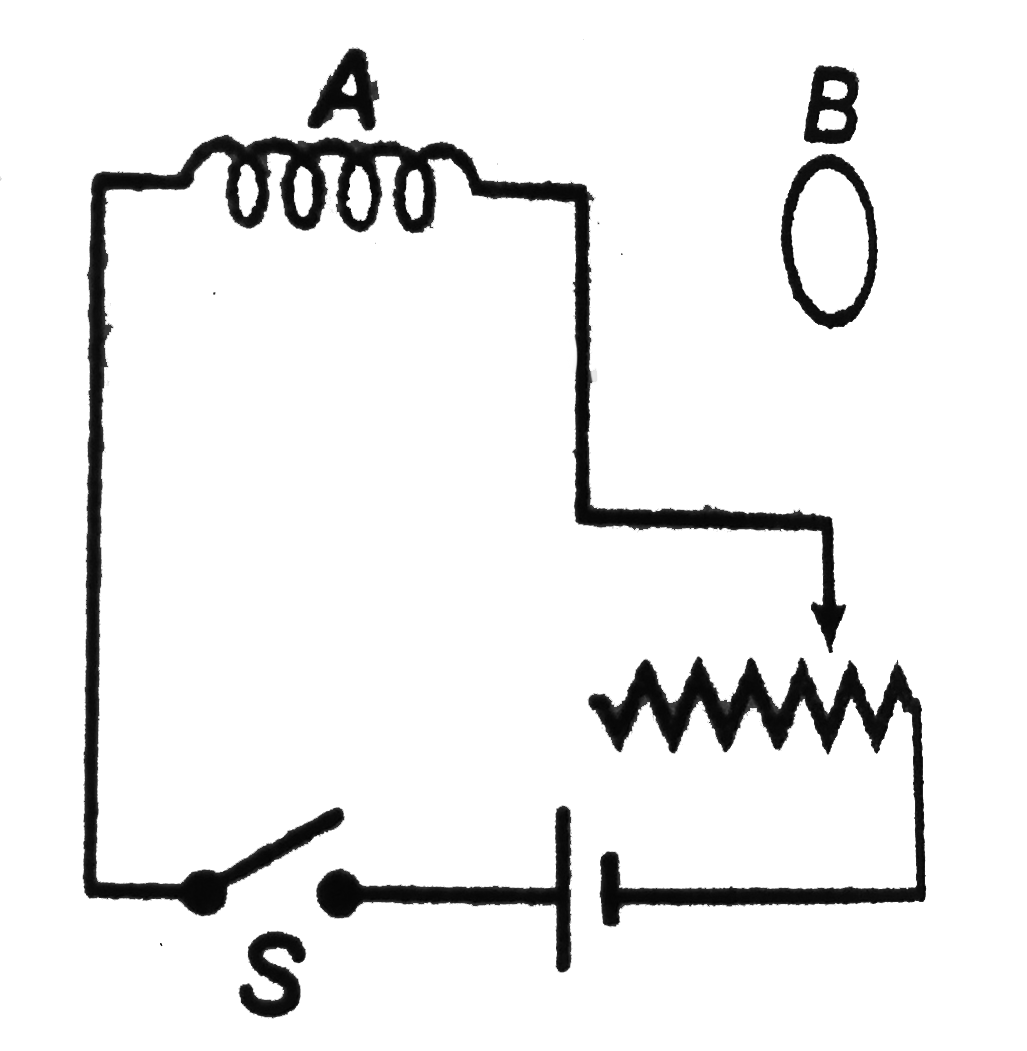 Ais attracted towards ASBis repelled by ACis initially repelled and then attractedDis initially attracted and then repelled
Ais attracted towards ASBis repelled by ACis initially repelled and then attractedDis initially attracted and then repelled
The ring B is coaxial with a solenoid A as shown in figure. As the switch S is closed at t=0, the ring B

View SolutionA ring of the radius r is suspended from a point on its circumference. If the ring is made to oscillate in the plane of the figure, then the angular frequency of these small oscillations is
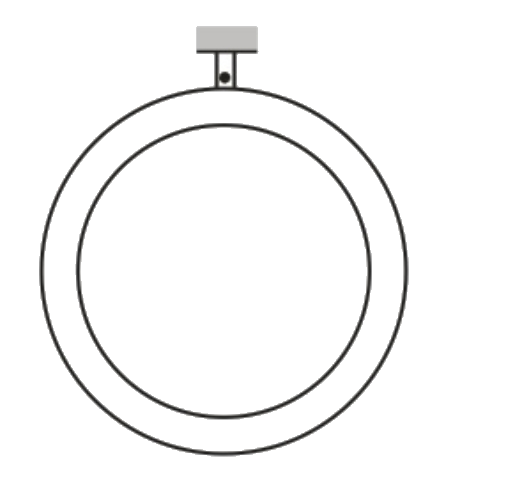
View SolutionA ring of the radius r is suspended from a point on its circumference. If the ring is made to oscillate in the plane of the figure, then the angular frequency of these small oscillations is

View SolutionA ring of radius R with a uniformly distributed charge q as shown in figure. A charge q0, is now placed at the centre of the ring. Find the increment in-the tension in ring.

View SolutionA ring of radius r is suspended from a point on its circumference. Determine its angular frequency of small oscillations.

View SolutionA ring of radius r is suspended from a point on its circumference. Determine its angular frequency of small oscillations.

View Solution

