Two chambers containingm, and m, gram of a gas at pressures and respectively are put in communication with each other, temperature remaining constant. The common pressure reached will be
The correct Answer is:A
According to Boyle.s law, PV=k(a constant)
or
So,
Similarly,
Total volume
Let P be the common pressure and be the common density ofmixture. Then
Similar Questions
Two chambers containing m1 and m2 kg of gas at pressure p1 and p2 are later connected. What will be pressure of the mixture.
View SolutionTwo containers of equal volume contain the same gas at pressure P1 and P2 and absolute temperature T1 and T2, respectively. On joining the vessels, the gas reaches a common pressure P and common temperature T. The ratio P/T is equal to
View Solution
Knowledge Check
Two cylinder having m1g and m2g of a gas at pressure P1 and P2 respectively are put in cummunication with each other, temperature remaining constant. The common pressure reached will be
Am1m2P2P2m1+P1m2BP1P2m1P2m1+P1m2Cm1m2(P1+P2)P2m1+P1m2DP1P2(m1+m2)P2m1+P1m2Two cylinder having m1g and m2g of a gas at pressure P1 and P2 respectively are put in cummunication with each other, temperature remaining constant. The common pressure reached will be
AP1P2(m1+m2)P2m1+P1m2BP1P2m1P2m1+P1m2Cm1m2(P1+P2)P2m1(P1+P2)Dm1m2P2P2m1+P1m2Two containers of equal volume contain the same gas at pressure P1 and P2 and absolute temperature T1 and T2, respectively. On joining the vessels, the gas reaches a common pressure P and common temperature T. The ratio P/T is equal to
AP1T1+P2T2BP1T1+P2T2(T1+T2)2CP1T2+P2T2(T1+T1)2DP12T1+P22T2
Two containers of equal volume contain the same gas at pressure P1 and P2 and absolute temperature T1 and T2, respectively. On joining the vessels, the gas reaches a common pressure P and common temperature T. The ratio P/T is equal to
View SolutionTwo idential container joined by a small pipe initially contain the same gas at pressure p0 and absolute temperature T0. One container is now maintained at the same temperature while the other is heated to 2T0. The common pressure of the gas
View SolutionTwo containers of equal volume contain the same gas at pressure P1 and P2 and absolute temperature T1 and T2, respectively. On joining the vessels, the gas reaches a common pressure P and common temperature T. The ratio P/T is equal to
View SolutionTwo idential container joined by a small pipe initially contain the same gas at pressure p0 and absolute temperature T0. One container is now maintained at the same temperature while the other is heated to 2T0. The common pressure of the gas
View SolutionV vs T curves at constant pressure P1 and P2 for an ideal gas are shown below
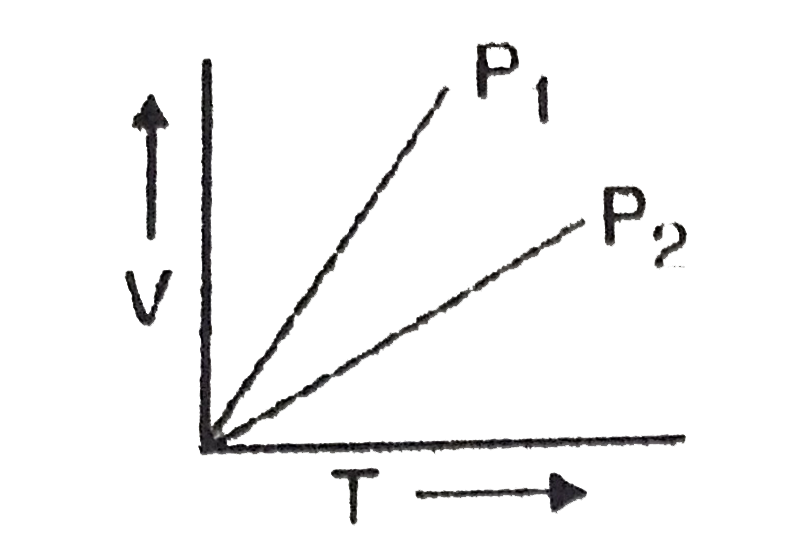
Which is correct ?
View Solution
