A long wire bent as shown in figure carries current I. If the radius of the semicircular portion is 'a' the magnetic field at the centre C is
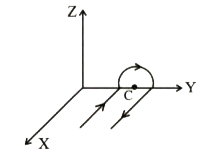
μ0I2πa(πˆi+2ˆk)
μ0I4πa(πˆi+2ˆk)
−μ0I4πa(πˆi+2ˆk)
μ0I4πa(πˆi−2ˆk)
The correct Answer is:C
Similar Questions
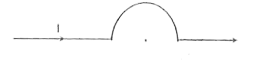
A long wire bent as shown in fig. carries current I. If the radius of the semicircular portion is a, the magnetic field at centre C is

View SolutionA long wire bent as shown in the figure carries current I=10A. If the radius of the semicircular portion is 1 m, the magnetic induction (in μT) at the centre C is
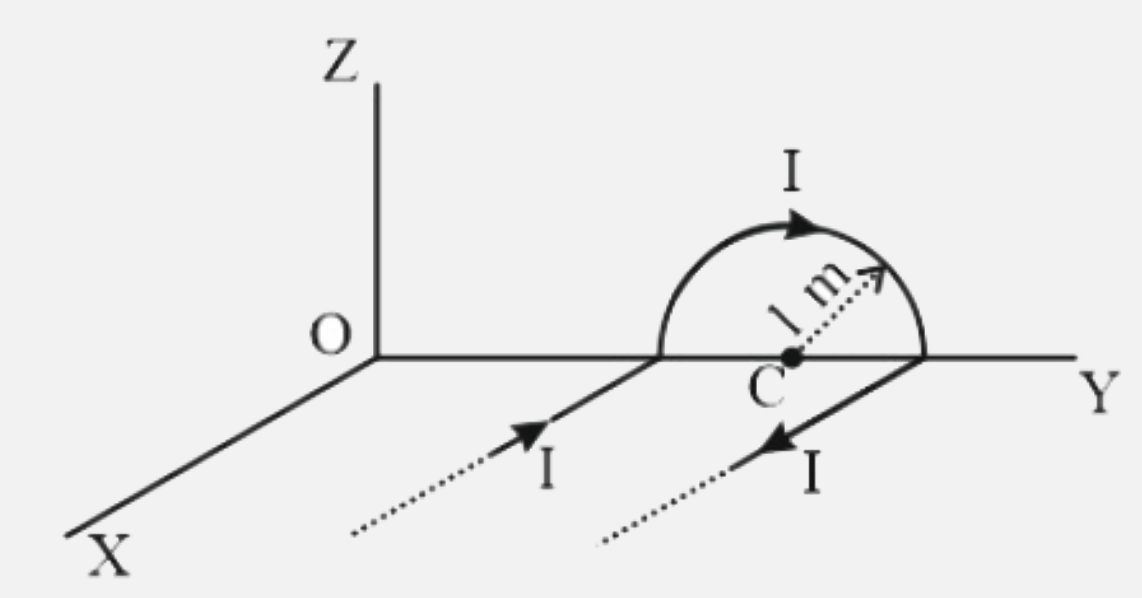
View Solution
Knowledge Check
A long wire bent as shown in fig. carries current I. If the radius of the semicircular portion is a, the magnetic field at centre C is
 Aμ0I4aBμ0I4πa√π2+4Cμ0I4a+μ0I4πaDμ0I4πa√(π2−4)
Aμ0I4aBμ0I4πa√π2+4Cμ0I4a+μ0I4πaDμ0I4πa√(π2−4)An infinitely long conductor is bent into a circle as shown in figure. It carries a current I ampere and the radius of loop is R meter. The magnetic induction at the centre of loop is
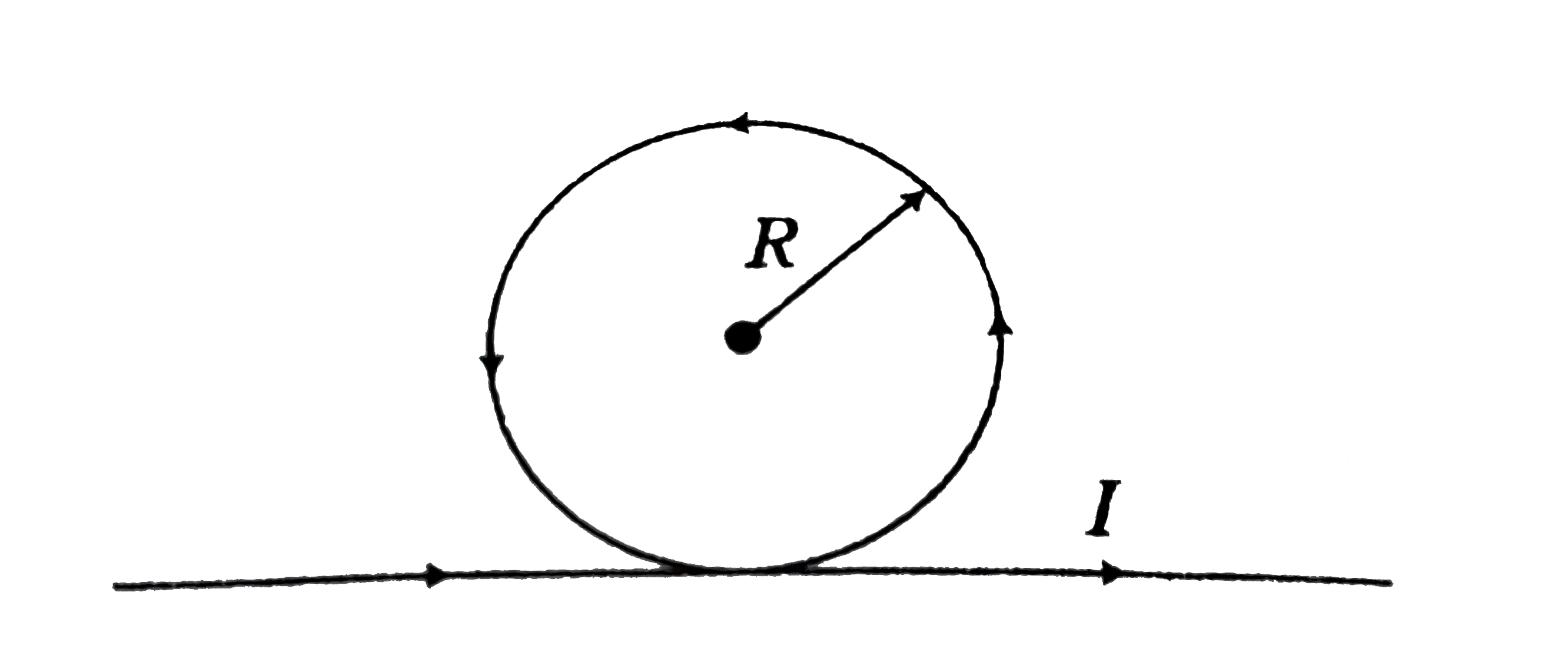 Aμ02I4πR(π+1)Bμ02I4πR(π−1)Cμ0I8πR(π+1)Dzero
Aμ02I4πR(π+1)Bμ02I4πR(π−1)Cμ0I8πR(π+1)DzeroA straight wire carrying a current 10A is bent into a semicircular arc of radius 5cm. The magnitude of magnetic field at the center is
A1.5×10−5TB3.14×10−5TC6.28×10−5TD19.6×10−5T

A long wire bent as shown in the figure carries current I=10A. If the radius of the semicircular portion is 1 m, the magnetic induction (in μT) at the center C is
View SolutionAn infinitely long straight conductor is bent into the shape as shown in figure. It carries the current I and radius of the circular loop is a, then the magnetic field at the centre of the loop is ______
View SolutionAn infinitely long conductor is bent into a circle as shown in figure. It carries a current I ampere and the radius of loop is R metre. The magnetic induction at the centre of loop is

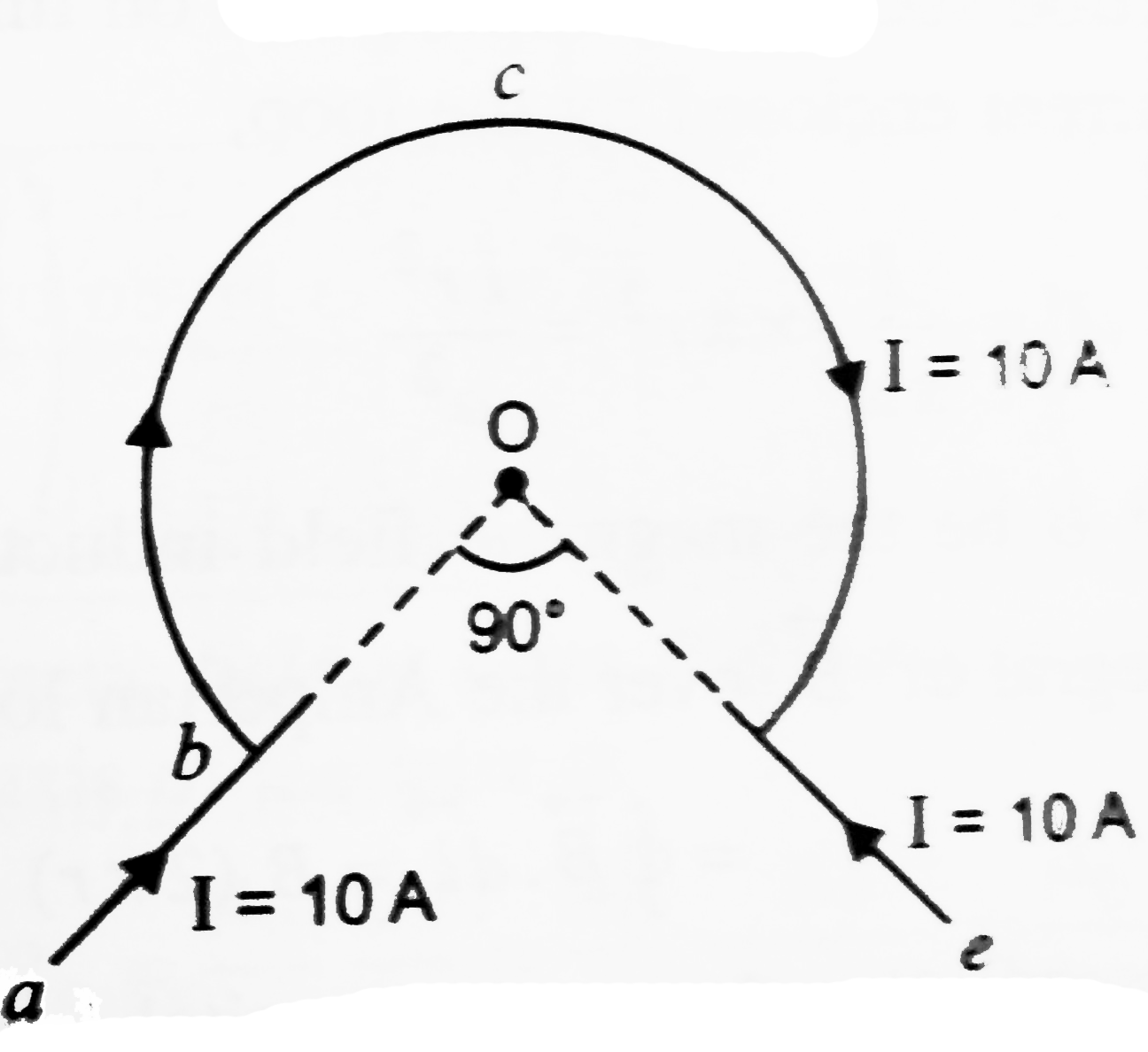
View SolutionThe wire shown in figure carries a current of 10A. Determine the magnitude of the magnetic field at the centre O.
Given radius of the bent coil is 3cm.
View SolutionA long current wire is bent in the shapes shown in figure. The circular portion has radius R. The magnetic induction at the center of the circular segment is

View Solution
