A gun of mass $m_{1}$ fires of a bullet of mass $m_{2}$ with a horizontal speed $v_{0}$ . The gun is fitted with a concave mirror of focal length f facing towards a receding bullet. Find the speed of separations of the bullet and the image just after the gun was fired.

Text Solution

Verified by Experts

Let $v_{1}$ be the speed of gun (or mirror) justa fter the firing of bullet. From conservation of linear momentum,

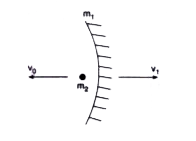
$m_{2} v_{0} = m_{1} v_{1}$
or $v_{1} = \frac{m_{2} v_{0}}{m_{1}}$ …..(i)
Now, $\frac{d u}{d t}$ = rate at which distance between mirror and bullet is increasing $= v_{1} + v_{0}$ ......(ii)
For a mirror $\frac{1}{v} + \frac{1}{u} = \frac{1}{f}$
Differentiating w.r.t. to time, $- v^{- 2} \frac{d v}{d t} - u^{2} \frac{d u}{d t} = 0$
$∴ \frac{d v}{d t} = (\frac{v^{2}}{u^{2}}) \frac{d u}{d t}$
Here, $\frac{v^{2}}{u^{2}} = m^{2} = 1$ (as at the time of firing bullet is at pole v = u).
$∴ \frac{d v}{d t} = \frac{d u}{d t} = v_{1} + v_{0}$ .......(iii)
Here, $\frac{d v}{d t}$ is the rate at which distance between image (of bullet) and mirror is increasing. So , if $v_{2}$ is the absolute velocity of image (towards right) then,
$v_{2} - v_{1} = \frac{d v}{d t} = v_{1} + v_{0}$
or $v_{2} = 2 v_{1} + v_{0}$ ......(iv)
Therefore, speed of separation of bullet and image will be,
$v_{r} = v_{2} + v_{0} = 2 v_{1} + v_{0} + v_{0}$
or $v_{r} = 2 (v_{1} + v_{0})$
Substituting value of $v_{1}$ from Eq. (i) we have, $v_{r} = 2 (1 + \frac{m_{2}}{m_{1}}) v_{0}$

Updated on:21/07/2023