A tank contains three layers of immiscible liquids. The first layer is of water with refractive index $\frac{4}{3}$ and thickness 8 cm. The second layer is an oil with refractive index $\frac{3}{2}$ and thickness 9 cm while the third layer is of glycerine with refractive index 2 and thickness 4 cm. Find the apparent depth of the bottom of the container.
$A tank contains three layers of immiscible liquids. The first layer is of water with refractive index (4)/(3) and thickness 8 cm. The second layer is an oil with refractive index (3)/(2) and thickness 9 cm while the third layer is of glycerine with refractive index 2 and thickness 4 cm. Find the apparent depth of the bottom of the container.$

Text Solution

Verified by Experts

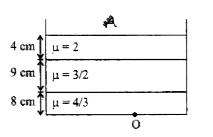
The system now comprises three slabs - one of water, one of oil and one of glycerine. As discussed in this Section and given by equation, the et shift of the system is the sum of the individual shifts in each of the slabs assuming they were in air.
Therefore, Net shift $s = t_{1} [1 - \frac{1}{μ_{1}}] + t_{2} [1 - \frac{1}{μ_{2}}] + t_{3} [1 - \frac{1}{μ_{3}}]$
$s = 8 [1 - \frac{3}{4}] + 9 [1 - \frac{2}{3}] + 4 [1 - \frac{1}{2}] = 7 c m$
The direction of the shift is in the direction of the incident rays which is upwards. Therefore, the apparent depth of the bottom of the container $= (4 + 9 + 8) - 7 = 14 c m$

Updated on:21/07/2023

Refractive index of glass is $\frac{3}{2}$ and the refractive index of water is $\frac{4}{3}$ . Then the refractive index of glass with respect to water is
A $\frac{3 / 2}{4 / 3}$
B $\frac{3}{2} \times \frac{4}{3}$
C $\frac{3}{2} + \frac{4}{3}$
D $\frac{3}{2} - \frac{4}{3}$
A beaker is filled with two immiscible transparent liquids of refractive indices $μ_{1}$ and $μ_{2}$ having thickness of layers $d_{1}$ and $d_{2}$ respectively. The apparent depth of the bottom of the beaker is
A $(\frac{d_{1} \times d_{2}}{d_{1} + d_{2}}) ((\frac{1}{μ_{1}}) + (\frac{1}{μ_{2}}))$
B $(μ_{1} \times μ_{2}) (d_{1} + d_{2})$
C $((\frac{d_{1}}{μ_{2}}) + (\frac{d_{2}}{μ_{1}}))$
D $⎛ ⎜ ⎝ \frac{\frac{d_{1}}{μ_{1}}}{\frac{d_{2}}{μ_{2}}} ⎞ ⎟ ⎠$
A vessel of depth 2d cm is half filled with a liquid of refractive index $μ_{1}$ and the upper half with a liquid of refractive index $μ_{2}$ . The apparent depth of the vessel seen perpendicularly is
A $d (\frac{μ_{1} μ_{2}}{μ_{1} + μ_{2}})$
B $d (\frac{1}{μ_{1}} + \frac{1}{μ_{2}})$
C $2 d (\frac{1}{μ_{1}} + \frac{1}{μ_{2}})$
D $2 d (\frac{1}{μ_{1} μ_{2}})$