A beaker is filled with two immiscible transparent liquids of refractive indices μ1 and μ2 having thickness of layers d1 and d2 respectively. The apparent depth of the bottom of the beaker is
(d1×d2d1+d2)((1μ1)+(1μ2))
(μ1×μ2)(d1+d2)
((d1μ2)+(d2μ1))
((d1μ1)+(d2μ2))
The correct Answer is:D
Step by step video & image solution for A beaker is filled with two immiscible transparent liquids of refractive indices mu_1 and mu_2 having thickness of layers d_1 and d_2 respectively. The apparent depth of the bottom of the beaker is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Three immiscibles transparent liquids with erefractive indices 3/2,4/3 and 6/5 are arranged one on top of another. The depth of the liquid are 3 cm, 4 cm and 6 cm respectively. The apparent depth of the vessel is
View SolutionTwo immiscible liquids of refractive index √2 and 2√2 are filled with equal height h in a vessel. Then apparent depth of bottom surface of the container given that outside medium is air
View SolutionA vessel of depth 2d cm is half filled with a liquid of refractive index μ1 and the upper half with a liquid of refractive index μ2. The apparent depth of the vessel seen perpendicularly is
View SolutionA tank contains three layers of immiscible liquids. The first layer is of water with refractive index 4/3 and thickness 8cm. The second layer is of oil with refractive index 3/2 and thickness 9cm while the third layer is of glycerine with refractive index 2 and thickness 4cm. Find the apparent depth of the bottom of the container.

View SolutionA thin convex lens made from crown glass (μ=3/2) has focal length f. When it is measured in two different liquids having refractive indiced 4/3 and 5/3, it has the focal length f1 and f2 respectively. The correct ralation between the focal lengths is
View SolutionA vessel is quarter filled with a liquid of refractive index μ. The remaining parts of the vessel is filled with an immiscible liquid of refractive index 3μ/2. The apparent depth of the vessel is 50% of the actual depth. The value of μ is
View SolutionA man observes a coin placed at the bottom of a beaker which contains two immiscible liquids of refractive indices 1.2 and 1.4 as shown in the figure. Find the depth of the coin below the surface, as observed from above.
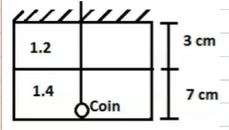
View SolutionA vessel of depth 2h is half filled with a liquid of refractive index 2√2 and the upper half with another liquid of refractive index √2. The liquids are immiscible. The apparent depth of the inner surface of the bottom of vessel will be:
View Solution
A cylinderical block of density d stays fully immersed in a beaker filled with two immiscible liquids of different densities d1 and d2 The block is in equilibrium with half of it in liquid 1 and the other half in liquid 2 as shown in the Fig. If the block is given a displacement downwards released, then neglecting friction study the following statements.
View Solution
A cylinderical block of density d stays fully immersed in a beaker filled with two immiscible liquids of different densities d1 and d2 The block is in equilibrium with half of it in liquid 1 and the other half in liquid 2 as shown in the Fig. If the block is given a displacement downwards released, then neglecting friction study the following statements.
View Solution
