A ray of light falls normally on a refracting face of a prism of refractive index 1.5. Find the angle of the prism if the ray just fails to emerge from the prism.

Text Solution

Verified by Experts

At first face of the prism as $i_{1} = 0^{\circ}, {\sin 0}^{\circ} = 1.5 {\sin r}_{1}$
i.e., $r_{1} = 0^{\circ}$
And as for a prism, $r_{1} + r_{2} = A$ so $r_{2} = A$ ….(i)
But at second face, as the ray just fails to emerge , i.e.,
$r_{2} = θ_{c}$ ....... (ii)

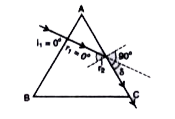
So from Eq. (i) and (ii), $A = r_{2} = θ_{c}$
But as $\sin^{- 1} [\frac{1}{μ}] = \sin^{- 1} [\frac{2}{3}] = 42^{\circ}$
So $A = 42^{\circ}$

|

Updated on:21/07/2023

Class 12 PHYSICS GEOMETRICAL OPTICS

Similar Questions

Knowledge Check

Question 1 - Select One
A monochromatic ray of light is incident normally on one of the refracting surfaces of a prism . The emergent ray grazes the second refracting surface . What is the angle of the prism if the refractive index of the material of the prism is $1.6$ ?
A $\frac{sin (\frac{A + δ}{2})}{sin (\frac{A}{2})}$
B $\frac{sin A}{sin δ}$
C $\frac{sin δ}{sin A}$
D $\frac{sin (A + δ)}{sin (A)}$
Question 2 - Select One
A ray of light is incident normally on one of the equal faces of a right isosceles prism of refractive index 1.5. The angle between incident and emergent rays is
A $45^{\circ}$
B $90^{\circ}$
C $180^{\circ}$
D $0^{\circ}$
Question 3 - Select One
When a ray of light is incident normally on one refracting surface of an equilateral prism (Refractive index of the material of the prism $= 1.5$
AEmerging ray is deviated by $30$
BEmerging ray is deviated by $45^{\circ}$
CEmerging ray just grazes the second refracting surface
DThe ray undergoes total internal reflection at the second refracting surface

Recommended Questions

Home
Ask Doubt
Profile