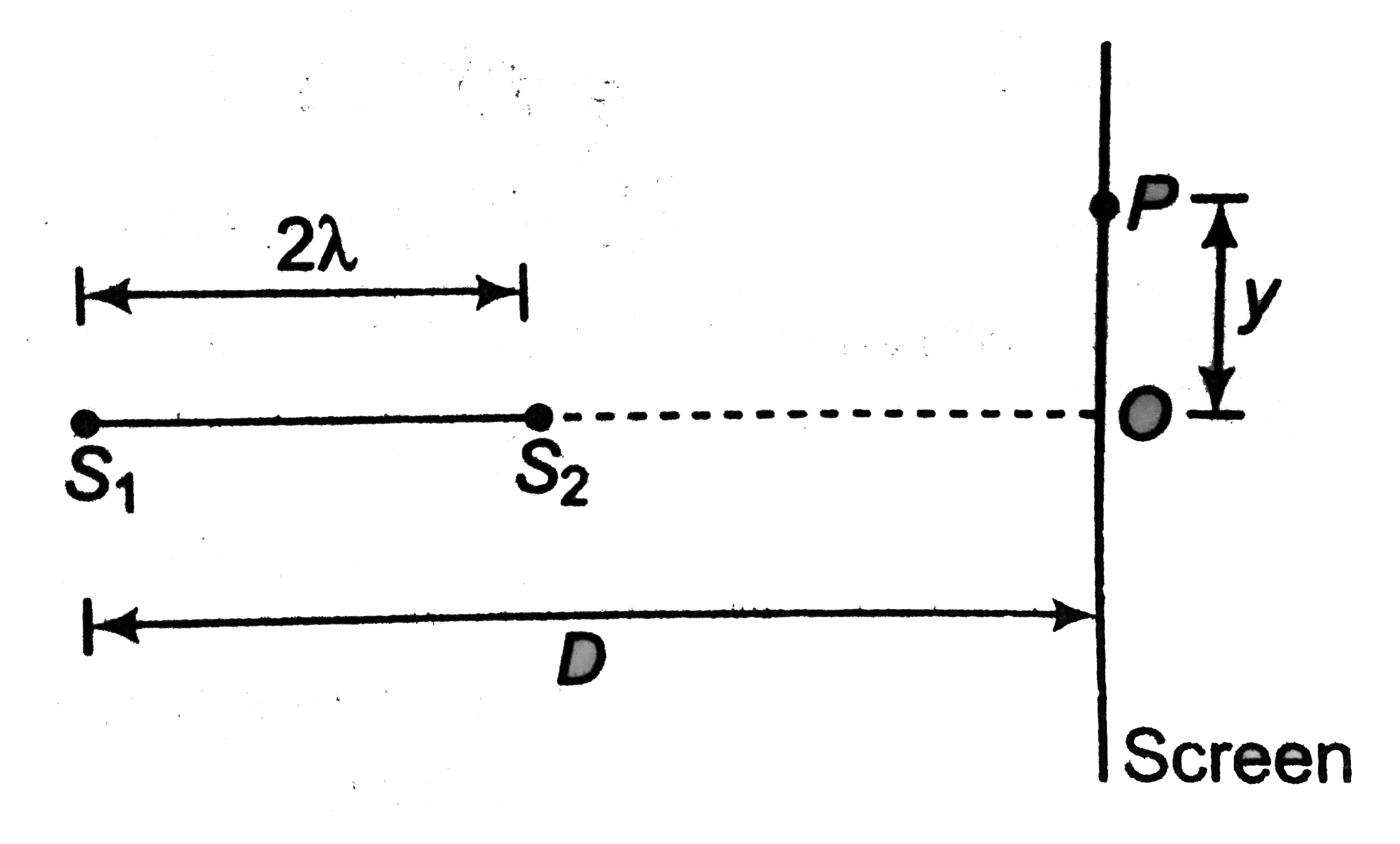
Two coherent narrow slits emitting light of wavelength λ in the same phase are placed parallel to each other at a small separation of 2λ. The light is collected on a screen S which is placed at a distance D(>>λ) from the slit S1 as shown in figure. Find the finite distance x such that the intensity at P is equal to intensity at O.
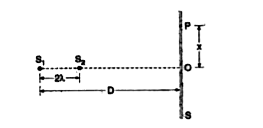
Path difference at O, S1O−S2O=2λ
i.e., maximum intensity is obtained at O. Next maxima will be obtained at point P where,
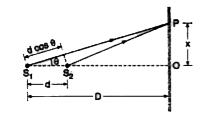
S1P−S2P=λ or dcosθ=λ
or (2λ)cosθ=λ or cosθ=12 ∴θ=60∘
Now in ΔS1PO,POS1O=tanθ or xD=tan60∘=√3 ∴x=√3D
Similar Questions
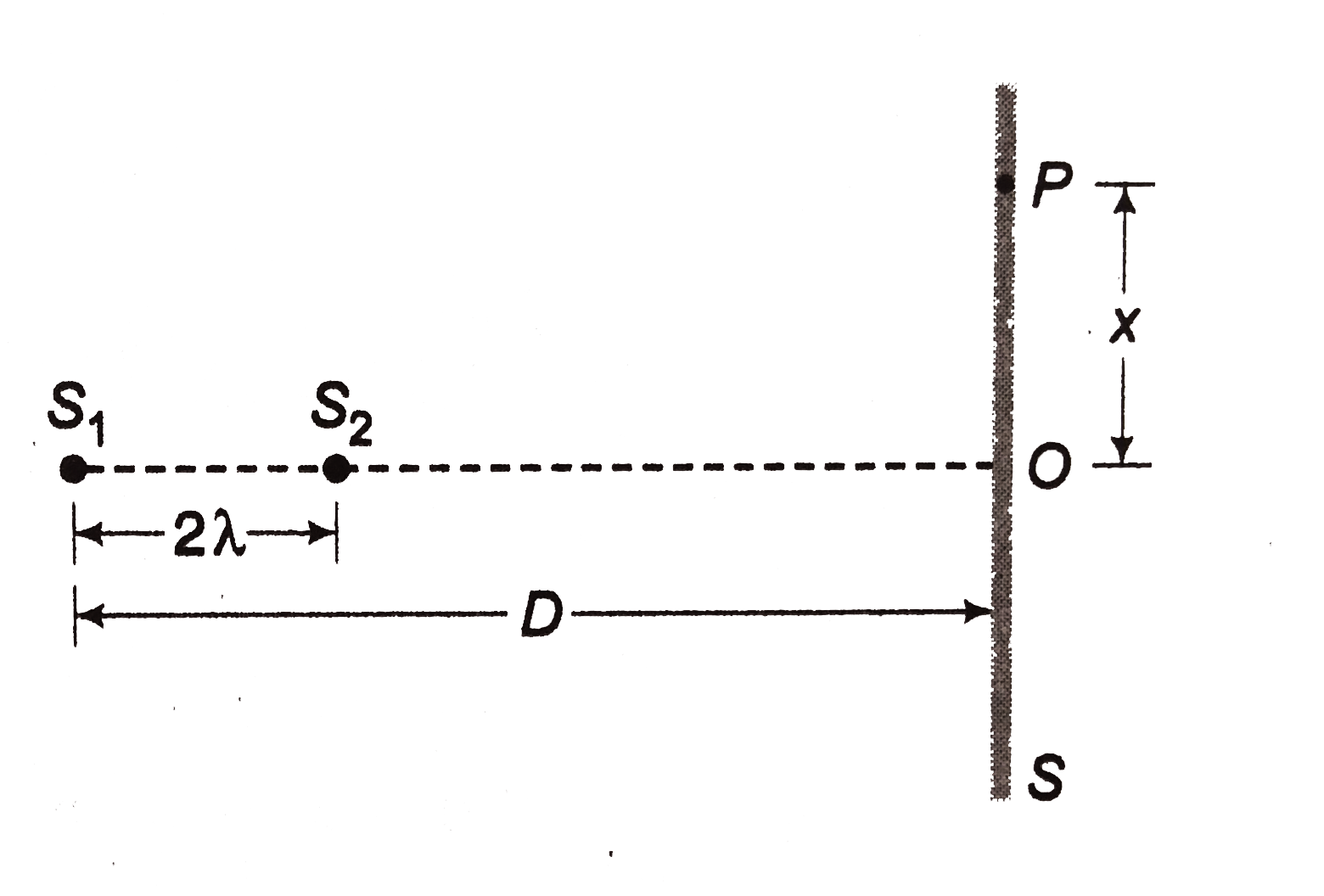
Two coherent narrow slits emitting light of wavelength λ in the same phase are placed parallel to each other at a small separation of 2λ. The light is collected on a screen S which is placed at a distance D(gtgtλ) from the slit S1 as shown in figure. Find the finite distance x such that the intensity at P is equal to intensity O.
.View SolutionTwo coherent narrow slits emitting light of wavelength λ in the same phase are placed parallel to each other at a small separation of 2λ. The light is collected on a screen S which is placed at a distance D(gtgtλ) from the slit S1 as shown in figure. Find the finite distance x such that the intensity at P is equal to intensity O.
.View Solution
Knowledge Check
- Question 1 - Select One
_E01_037_Q01.png)
Two coherent narrow slits emitting light of wavelength λ in the same phase are placed parallel to each other at a small separation of 3λ the light is collected on a screen S which is placed at a distance D(>>λ) from the slits the smallest distance x such that the P is a maxima.A√3DB√8DC√5DD√5D2 - Question 2 - Select One
Choose the most appropriate option.
Two coherent point sources S1andS2 vibrating in phase emit light of wavelength λ. The separation between them is 2λ. The light is collected ona screen placed at a distance D>>λ from the slit S1 as shown. The minimum distance, so that intensity at P is equal to intensity at O.
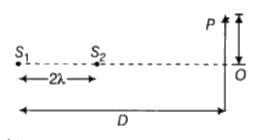A√2DB√3DC√8DD√5D
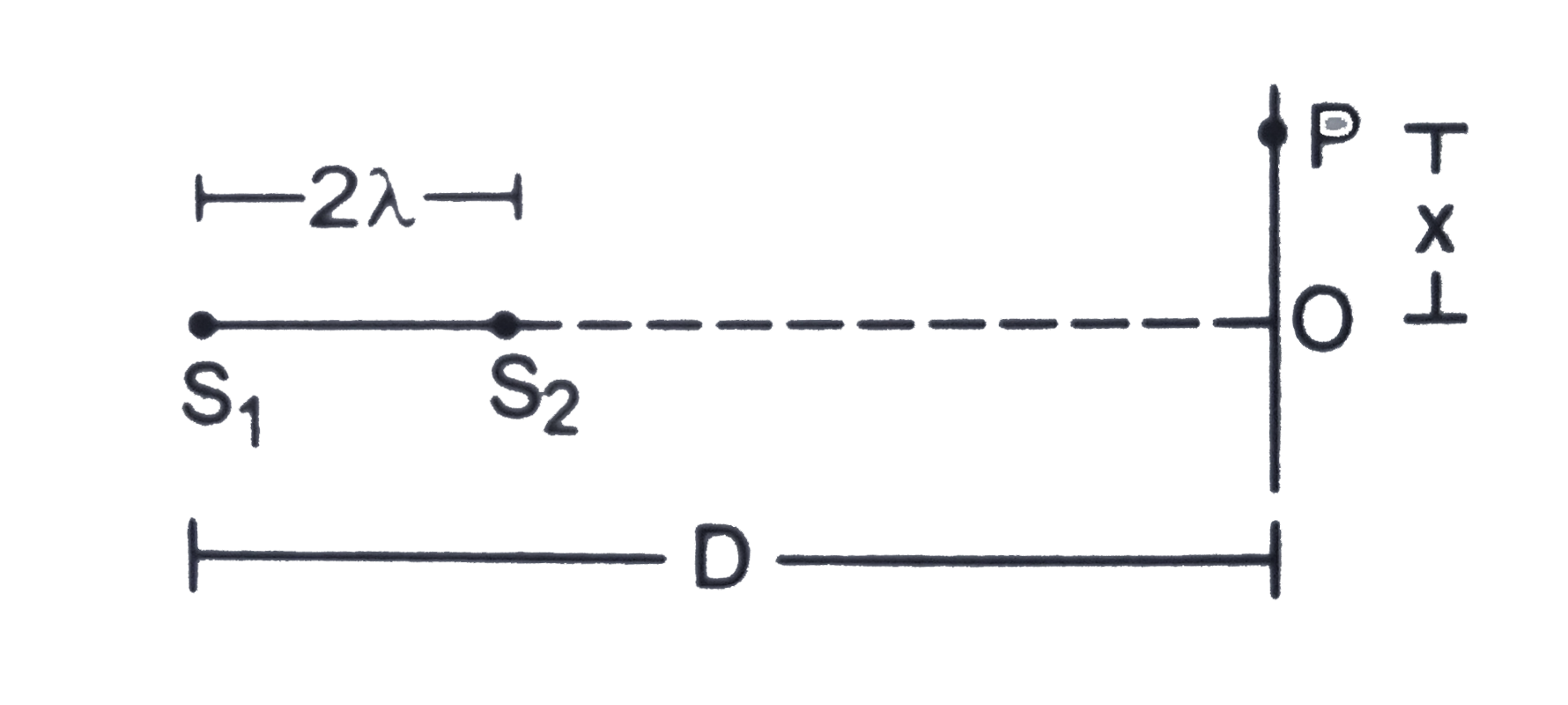
Two coherent narrow slits emitting sound of wavelength λ in the same phase are placed parallet to each other at a small separation of 2λ . The sound is delected by maving a delector on the screen at a distance D(>>λ) from the slit S1 as shows in figure. Find the distance y such that the intensity at P is equal to intensity at O .
View SolutionTwo coherent narrow slits emitting sound of wavelength λ in the same phase are placed parallet to each other at a small separation of 2λ . The sound is delected by maving a delector on the screen at a distance D(>>λ) from the slit S1 as shows in figure. Find the distance y such that the intensity at P is equal to intensity at O .
View SolutionTwo coherent narrow slits emitting sound of wavelength lamda in the same phase are placed parallel to each other at a small separation of 2λ. The sound is detected by moving a detector on the screen ∑ at a distance D(gtgtlamda) from the slit S1 as shown in figure. Find the distance x such that the intensity at P is equal to the intensity at O.
View SolutionTwo coherent narrow slits emitting wavelength λ in the same phase are placed parallel to each other at a small separation of 2λ, the sound is detected by moving a detector on the screen S at a distance D(>>λ) from the slit S1 as shown in Fig. 7.76. Find the distance x such that the intensity at P is equal to the intensity at O.
View SolutionTwo coherent point sources S1andS2 vibrating in phase emit light of wavelength λ . The separation between them is 2λ . The light is collected on a screen placed at a distance D>>λ from the slit S1 as shown. The minimum distance, so that intensity at P is equal to the intensity at O
View SolutionConsider the situation shown in figure-6.35. The two slits S1 and S2 placed symmetrically around the central line are illuminated by a monochromatic light of wavelength λ. The separation between the slits is d. The light transmitted by the slits falls on a screen E1 placed at a distance D from the slits. The slit S3 is at the central line and the slit S4 is at a distance z from S3. Another screen E2 is placed a further distance D away from E1. Find the ratio of the maximum to minimum intensity observed on E2 if z is equal is : (a)λD2d (b)λDd (c)λD4d
View Solution