When light is incident on a medium at angle i and refracted into a second medium at an angler, the graph of sin ivs sinr is as shown in the graph. From this, one can conclude that
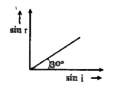
Velocity of light in the second medium is 1.73 times the velocity of light in the first medium
Velocity of light in the first medium is 1.73 times the velocity in the second medium
The critical angle for the two media is given by sin ic=13
sin ic=12
The correct Answer is:B
From graph tan30∘=sinrsini=11μ2
1μ2=√3, μ2μ1=v1v2=1.73, v1=1.73v2
Also from μ=1sinC, sinC=1RarerμDenser, sinC=11μ2=1√3
Similar Questions
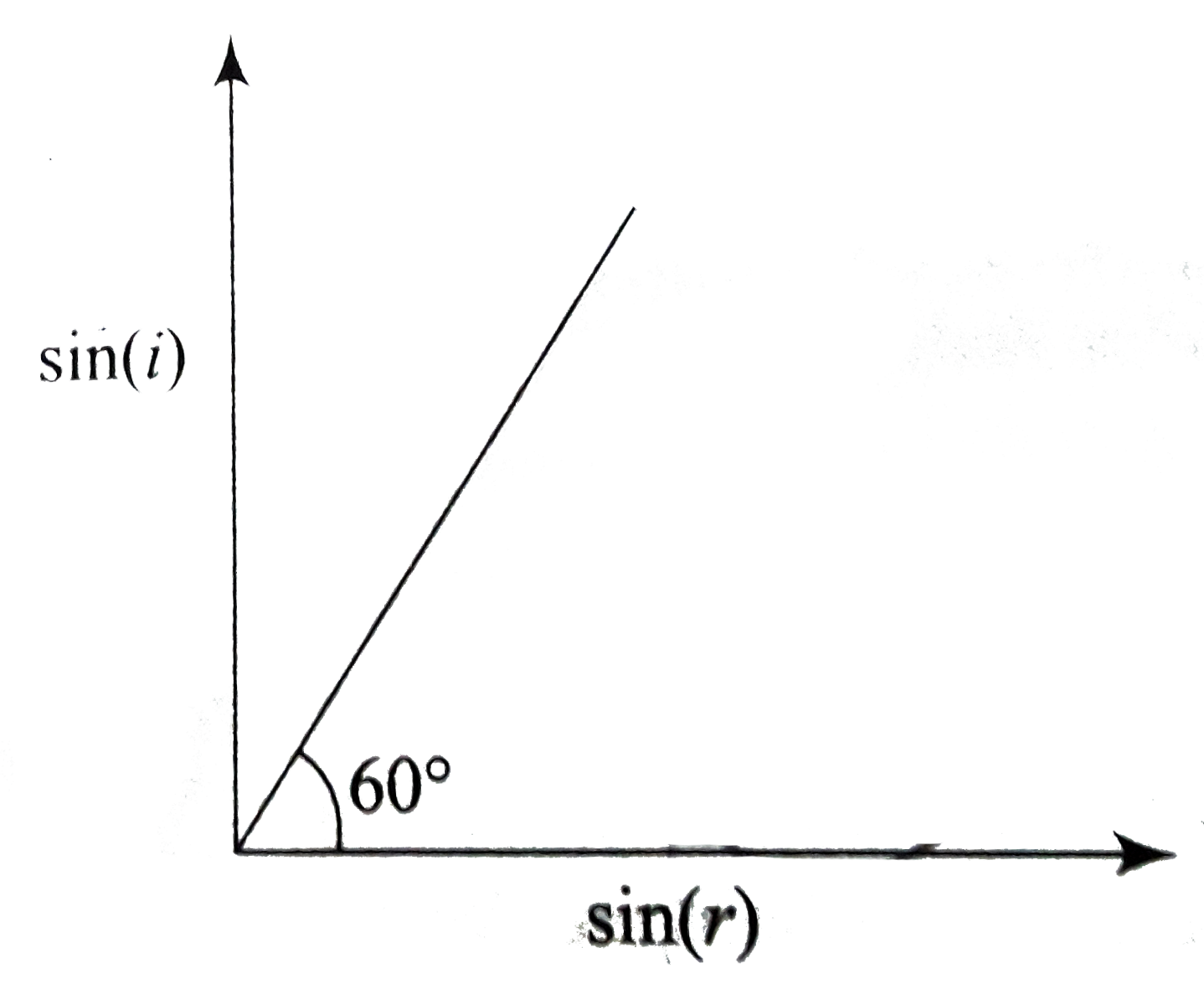
When light is incident on a medium at angle i and refracted into a second medium at an angle r, the graph of sinr versus sini is as shown. From this one can conclude that

(i) the velocity of light in second medium is √3 times the velocity of light in the first medium
(ii) the velocity of light in the first medium is √3 times the velocity of ligth in second medium
(iii) the critical angle of the two media is given by siniC=1√3
(iv) the critical anlge of the two media is given by siniC=1√2
View SolutionA ray of light is incident on a medium with angle of incidence I and refracted into a second medium with angle of refraction r. The graph of sin(i)vssin(R) is as shown in figure. Then the velocity of light in the first medium in n times the velocity of light in the second medium. What shoul be th evalue of n?
View Solution
Knowledge Check
When light is incident on a medium at angle i and refracted into a second medium at an angle r, the graph of sinr versus sini is as shown. From this one can conclude that

(i) the velocity of light in second medium is √3 times the velocity of light in the first medium
(ii) the velocity of light in the first medium is √3 times the velocity of ligth in second medium
(iii) the critical angle of the two media is given by siniC=1√3
(iv) the critical anlge of the two media is given by siniC=1√2A(i), (ii)B(ii), (iii)C(i), (iii)D(i), (iv)A ray of light is incident on a medium with angle of incidence I and refracted into a second medium with angle of refraction r. The graph of sin(i)vssin(R) is as shown in figure. Then the velocity of light in the first medium in n times the velocity of light in the second medium. What shoul be th evalue of n?
 A√3B1/√3C√3/2D2/√3
A√3B1/√3C√3/2D2/√3When light is incident on a medium of refractive index μ from rarer medium at an angle 'i' and is refracted at an angle 'r', then Snell's law gives
Aμ=sinisinrBμ=sinrsiniCμ=sini×sinrD1μ=sinisinr
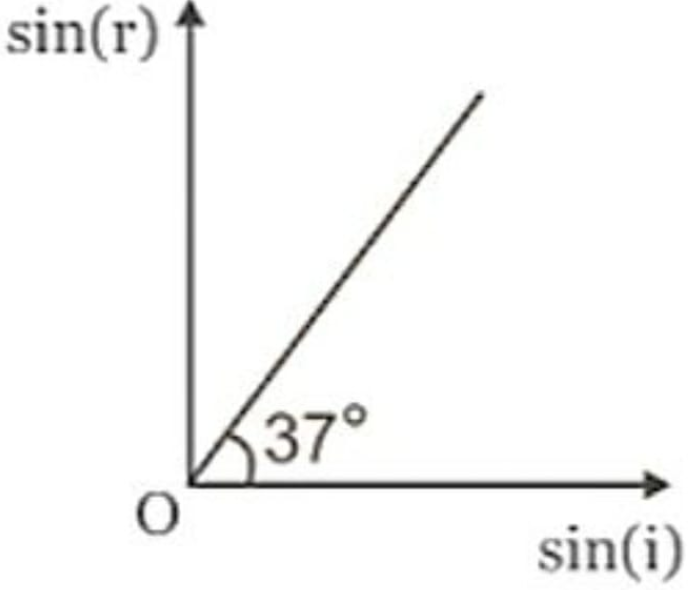
A ray of light travelling in medium. A is incident on the plane interface of two medium W and B and gets refracted into the medium B. The angle of incidence is I and that of refraction is r. The graph between sin(i) and sin(r) is a shown in the diagram . The correct Statement among the following is
View SolutionA ray of light is incident on the surface of seperation of a medium at an angle 45∘ and is refracted in the medium at an angle 30∘. What will be the velocity of light in the medium?
View SolutionA ray of light travelling in medium. A is incident on the plane interface of two medium W and B and gets refracted into the medium B. The angle of incidence is I and that of refraction is r. The graph between sin(i) and sin(r) is a shown in the diagram . The correct Statement among the following is

View SolutionA ray of light is incident on the surface of separation of a medium at an angle 45∘ and is refracted in the medium at an angle 30∘. What will be the speed of light in the medium?
View SolutionA ray of light is incident on the surface of separation of a medium at an angle 45∘ and is refracted in the medium at an angle 30∘. What will be the velocity of light in the medium?
View Solution
