Assertion: Two point coherent sources of light S1 and S2 are placed on a line as shown. P and Q are two points on that line. If at point P maximum intensity is observed then maximum intensity should also be observed at Q.
Reason : In the figure of assertion the distance |S1P−S2P| is equal to distance |S2Q−S1Q|.
If both assertion and reason are true and reason is the correct explanation of assertion .
If both assertion and reason are true but reason is not the correct explanation of assertion .
If assertion is true but reason is false.
If both assertion and reason are false.
The correct Answer is:d
Change in path of light does not change the wavelength neither does it separate the wavelengths of different colours. The reason is false. Dispersion can be due to diffraction.
Similar Questions
Statement I: Two point coherent sources of light S1 and S2 are placed on a line as shown in figure. P and Q are two points on that line. If at point P maximum intensity is observed, then maximum intensity should also be observed at Q.

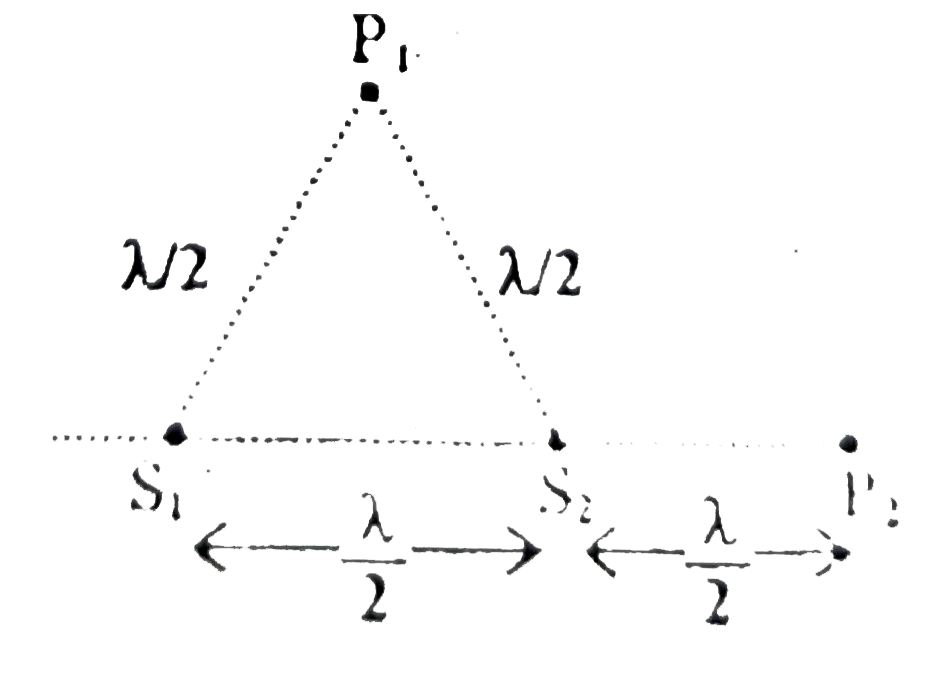
Statement II: In figure the distance |S1P−S2P| is equal to distance |S1Q−S2Q|.View SolutionS1 and S2 are two equally intense coherent point second sources vibrating in phase. The resultant intensity at P1 is 80SI units then resultant intensity at P2 in SI units will be
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Statement I: Two point coherent sources of light S1 and S2 are placed on a line as shown in figure. P and Q are two points on that line. If at point P maximum intensity is observed, then maximum intensity should also be observed at Q.

Statement II: In figure the distance |S1P−S2P| is equal to distance |S1Q−S2Q|.AStatement I is True, statement II is True, Statement II is a correct explanation for Statement I.BStatement I is Ture, Statement II is Ture, Statement II is NOT a correct explanation for Statement I.CStatement I is True, Statement II is False.DStatement I is False, Statement II is True. - Question 2 - Select One
S1andS2 are two coherent sources. The intensity of both sources are same. If the intensity at the point of maxima is 4Wm−2, the intensity of each source is
A1Wm−2B2Wm−2C3Wm−2D4Wm−2 - Question 3 - Select One
In the case of light waves from two coherent sources S1 and S2, there will be constructive interference at an arbitrary point P, the path difference S1P−S2P is
A(n+12)λBnλC(n−12)λDλ2
S1 and S2 are two equally intense coherent point second sources vibrating in phase. The resultant intensity at P1 is 80SI units then resultant intensity at P2 in SI units will be
 View Solution
View SolutionIn an AP,Sp=q,Sq=p . Then Sp+q is equal to :
View Solution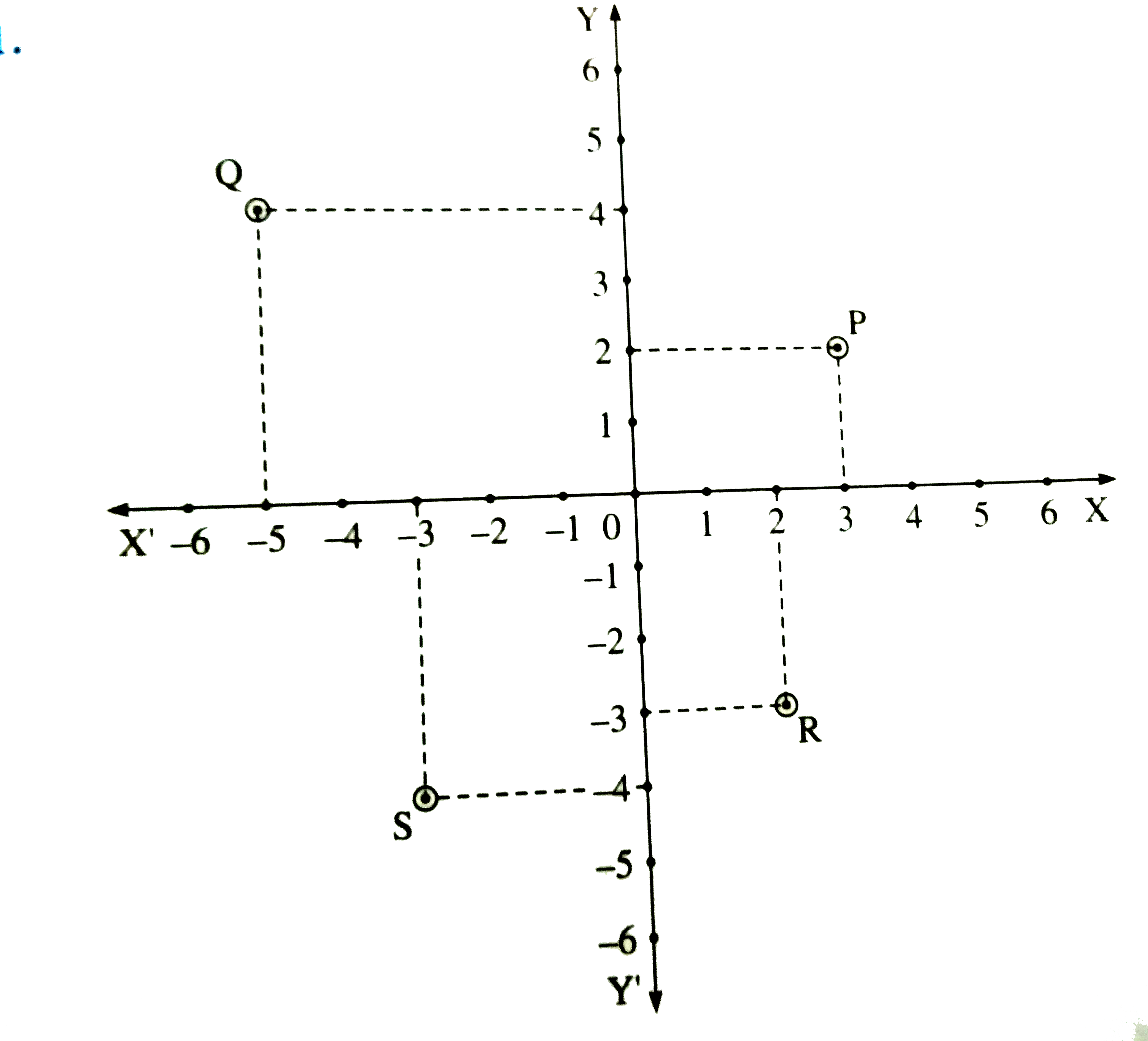
Observe the figure and write the coordinates of points P,Q,R and S.View SolutionIn the case of light waves from two coherent sources S1 and S2, there will be constructive interference at an arbitrary point P, the path difference S1P−S2P is
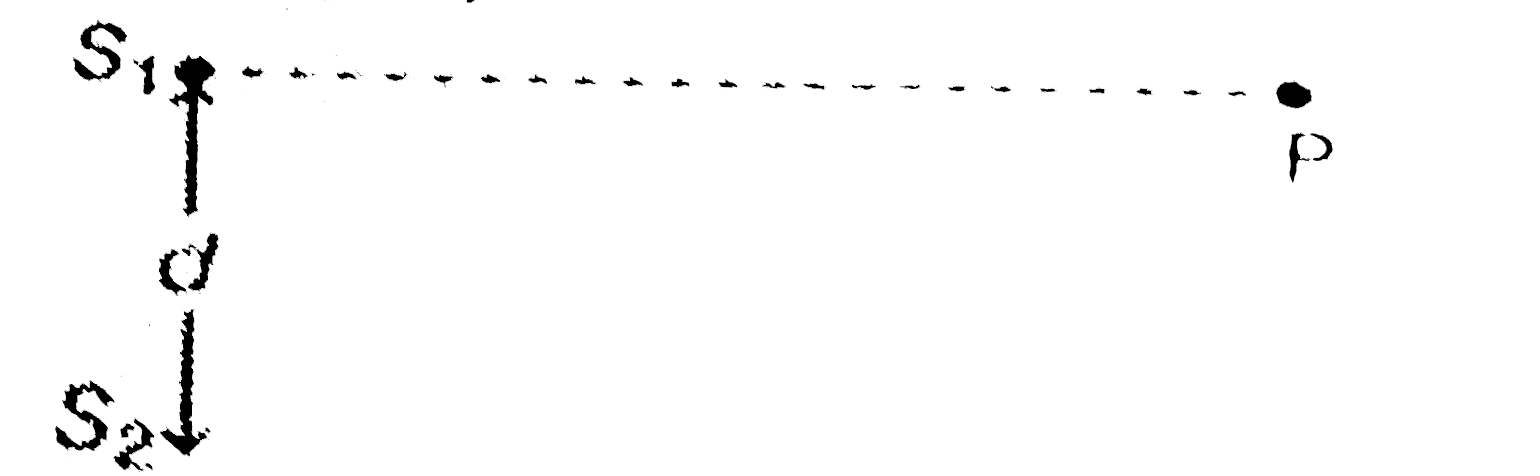
View SolutionConsider two coherent monochromatic (wavelength λ) sources S1andS2 separated by a distance d. The ratio of intensity of S1 and that of S2 at point P is 4. The distance of P from S1 if the resultant intensity at point P is equal to 94, times the intensity due to S1 is : (n is a positive integer )
 View Solution
View Solution

