A charge of 1 coulomb is placed at one end of a nonconductiong rod of length 0.6m. The rod is rotated in a vertical plane about a horizontal axis passing through the other end of the rod with angular frequency . Find the magnetic field at a point on the axis of rotation at a distance of 0.8 m from the centre of the path
Now half of the charge is removed from one end placed on the other end . The rod is rotated in a vertical plane about a horzontal axis passing through the mid point of the rod with the same angular frequency. Calculate the magnetic field at a point on the axis at a distance of 0.4 m from the centre of the rod
As revolving charge q is equivalent to a current
and field at a distance x from the centre on the axis of a current-carrying coil is given by
So,
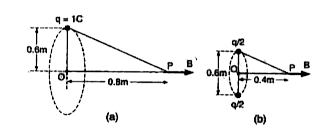
Now, if hald of the charge is placed at the other end and the rod is rotated at the same frequency
However, according to the given problem in the situation
So,
Similar Questions
A charge of 1 coul. is placed at one end of a non-conducting rod of length 0.6m. the rod is rotated in a vertical plane about a horizontal axis passing through the other end of the rod with angular frequency 104πradian/sec. Find the magnetic field at a point on the axis ofrotation at a distance of 0.8 from the centre of the path. Now half of the charge is removed from one end and placed on the other end. The rod is rotated in a vertical plane about horizontal axis passing through the mid-point of the rod with the same angnlar frequency. Calculate the magnetic field at a point on the axis at a distance of 0.4m form the centre of the rod.
View SolutionA charge of 1C is placed at one end of a non conducting rod of length 0.6m. The rod is rotated in a vertical plane about a horizontal axis passing through the other end of the rod with angular frequency 104πrad/s. Find the magnetic field at a point on the axis of rotation at a distance of 0.8m from the centre of the path.
View Solution
Knowledge Check
A uniform metal rod is rotated in horizontal plane about a vertical axis passing through its end at uniform rate. The tension in the rod is
Asame at all pointsBdifferent at differen points and maximum at centre of rodCdifferent at different points and minimum at axis of rotation.Ddifferent at different points and maximum at axis of rotationif rod is rotated about an axis passing through its mid-point , the potential difference between the ends of rod is
ABωL24BBωL22C3BωL24DzeroTwo balls of masses m and 2m are attached to the ends of a light rod of length L. The rod rotates with an angular speed ω about an axis passing through the center of mass of system and perpendicular to the plane. Find the angular momentum of the system about the axis of rotation.
A23mωL2B13ω2LmC23ω2LmD13Lm
A charge of 1 coulumb is placed is one end of a non-conducting rod of length 0.6m.The rod is rotated in a vertical plane about a horizontal axis passing through the other end of the rod with an angular velocity 104πrad/sec.Find the magnetic field at a point on the axis of rotation of a distance of 0.8m from the centre of the path is Nπ×10−4T,then find value of N.
View SolutionA charge of 1 coulumb is placed is one end of a non-conducting rod of length 0.6m.The rod is rotated in a vertical plane about a horizontal axis passing through the other end of the rod with an angular velocity 104πrad/sec.Find the magnetic field at a point on the axis of rotation of a distance of 0.8m from the centre of the path is Nπ×10−4T,then find value of N.
View SolutionA uniform rod of mass m and length L is free to rotate in the vertical plane about a horizontal axis passing through its end. The rod initially in horizontal position is released. The initial angular acceleration of the rod is:

View SolutionTwo balls of masses m and 2m are attached to the ends of a light rod of length L. The rod rotates with an angular speed ω about an axis passing through the center of mass of system and perpendicular to the plane. Find the angular momentum of the system about the axis of rotation.
View SolutionTwo balls of masses m and 2m are attached to the ends of a light rod of length L. The rod rotates with an angular speed ω about an axis passing through the center of mass of system and perpendicular to the plane. Find the angular momentum of the system about the axis of rotation.
View Solution
