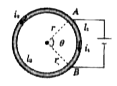
A battery is connected between two points A and B on the circumference of a uniform conducting ting of radius rand resistance R. One of the arcs AB of the ring subtends an angle θ at centre. The value of the magnetic induction at the centre due to the current in the ring is
Proportional to (180∘−θ)
Inversely proportional to r
Zero,only if θ=180∘
Zero for all values of θ
The correct Answer is:D
Directiojns of current in two parts are different, so directions of magnetic fields due to these currents are diffeerent
Applying Ihm.s law across AB
i.e.i1R1=i2R2=i1l1=i2l2............(i)
Also B1=μ04πi1l1r2andB2=μ04πi2l2r2 ∴B1B2=i1l1i2l2=1 using (i)
Hence two field are equal but of opposite direction. So, resultant magnetic induction at the centre ios zero and is independent of θ
Similar Questions
A battery is connected between two points A and B on the circumference of a uniform conducting ring of radius r and r
View SolutionA battery is connected between two points AandB on the circumference of a uniform conducting ring of radius r and resistance R . One of the arcs AB of the ring subtends an angle θ at the centre . The value of the magnetic induction at the centre due to the current in the ring is
View Solution
Knowledge Check
A battery is connected between two points AandB on the circumference of a uniform conducting ring of radius r and resistance R . One of the arcs AB of the ring subtends an angle θ at the centre . The value of the magnetic induction at the centre due to the current in the ring is
Aproportional to 2(180∘−θ)Binversely proportional to rCzero , only if θ=180∘Dzero for all values of θIn the figure shown, the magnetic induction at the centre of the arc due to the current in portion AB will be
 Aμ0irBμ0i2rCμ0i4rDzero
Aμ0irBμ0i2rCμ0i4rDzeroA current - carrying wire of certain length is bent to form an arc that substends an angle θ at the centre. Let B be the magnetic field at the centre due to this wire. The correct graph between B and θ is
A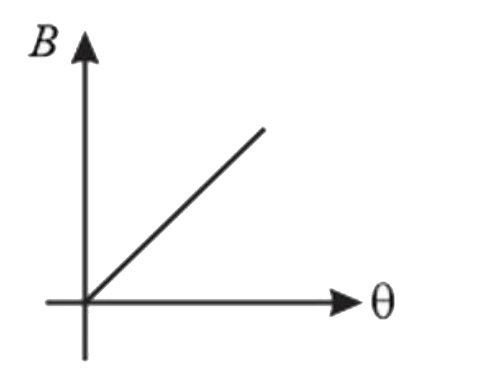 B
B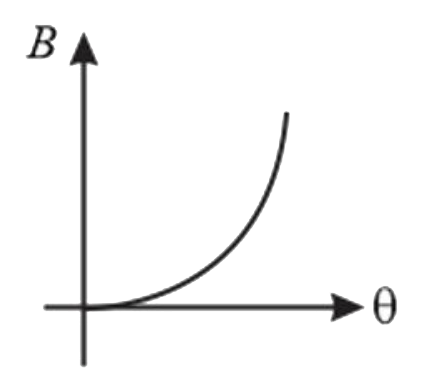 C
C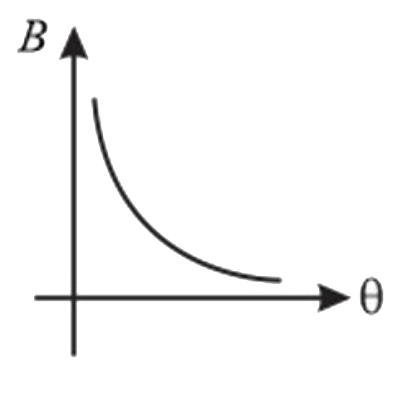 D
D
A battary is connected between two points A and B on the circumference of a uniform conducting ring of radius r and resistance R as shown in Fig. One of the arcs AB of the ring subtends angle θ at the centre. Show that that the magnetic field at the centre of the coil is zero and independent θ.
View SolutionIn the figure shown, the magnetic induction at the centre of the arc due to the current in portion AB will be

View SolutionA current - carrying wire of certain length is bent to form an arc that substends an angle θ at the centre. Let B be the magnetic field at the centre due to this wire. The correct graph between B and θ is
View SolutionAn arc of length of length 19 cm of a circle of radius 30 cm, subtends an angle θ at the centre O. The value of θ is:
View SolutionAn arc of length of length 19 cm of a circle of radius 30 cm, subtends an angle θ at the centre O. Then value of θ is:
View Solution
