A very small circular loop of area 5×10−4m2, resistance 2 ohm and neglogible inductance is initially coplanar and concentric with a much larger fixed circular loop of radius 0.1 m. A constant current of 1 ampere is passed in the bigger loop and the smaller loop is rotated with angular velocity ω rad/s about a diameter Calculate (a) the flux linked with the smaller loop (b) induced emf and induced current in the smaller loop as a function of time.
(a) The situation is shown in figure. The field at the centre of larger loop is given by
B1=μ04π2πIR=10−72π×10.1=2π×10−6Wbm−2
This magnetic field B1 is initially along the normal to the area of smaller loop. Now as the smaller loop (and hence normal to its plane) is rotating at angular velocity ω, so in time it turn by an angle θ=ωt w.r. to →B and hence the flux linked with the smaller loop at time t,
ϕ2=B1S2cosθ=(2π×10−6)(5×10−4)cosωt
i.e., ϕ2=π×10−9cosωtWb

(b) The induced emf in the smaller loop,
e2=−dϕ2dt=−ddt(π×10−9cosωt)
i.e., e2=π×10−9ωsinωt volt
(c) The induced current in the smaller loop, I2=e2R=12πωsinωt×10−9 ampere
Similar Questions
A very small circular loop of area 5×10−4m2 , resistance 2Ω and negligible inductance is initially coplanar and concentric with a much larger fixed circular loop of radius 0.1m . A constant current of 1A is passed in the bigger loop and the smaller loop is rotated with angular velocity ωrad/sec about a diameter. Calculate (a) the flux linked with the smaller loop, (b) induced emf (c) induced current in the smaller loop, as a function of time.
View SolutionA very small circular loop of area 5×I0−4m2 , resistance 2Ω and negligible inductance is initially coplanar and concentric with a much larger fixed circular loop of radius 0.Im . A constant current of IA is passed in the bigger loop and the smaller loop is rotated with angular velocity ωrad/sec about a diameter. Calculate (a) the flux limked with the smaller loop, (b) indced emf (c) induced current in the smaller loop, as a function of time.
View Solution
Knowledge Check
A very small circular loop of radius a is initially (at t = 0) coplanar and concentric with a much larger fixed circular loop of radius b. A constant current I flows in the larger loop. The smaller loop is rotated with a constant angular speed ω about the common diameter. The emf induced in the smaller loop as a function of time t is
Aπa2μ0I2bωcos(ωt)Bπa2μ0I2bωsin(ω2t2)Cπa2μ0I2bωsin(ωt)Dπa2μ0I2bωsin2(ωt)A very small circular loop of radius a is initially (at t = 0) coplanar and concentric with a much larger fixed circular loop of radius b. A constant current I flows in the larger loop. The smaller loop is rotated with a constant angular speed ω about the common diameter. The emf induced in the smaller loop as a function of time t is
Aπa2μ0I2bωcosωtBπa2μ0I2bωsinω2t2Cπa2μ0I2bωsinωtDπa2μ0I2bωsin2ωtA very small circular loop of radius a is initially coplanar & concentric with a much larger circular loop of radius b (>>a). A constant current is passed in the large loop which is kept fixed in space & the small loop is rotated with angular velocity omega about a diameter. The resistance of the small loop is R & its self inductance is negligible. The current in the larger loop is clockwise.
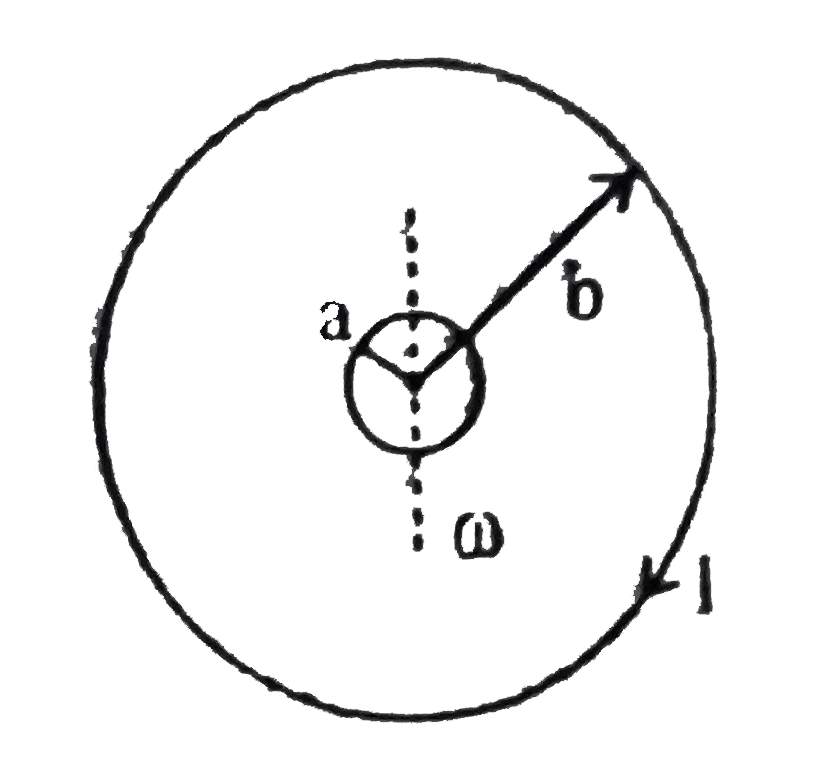
Find the current in the small loop as a function of time.Aπa2μ0Iωsinωt2bRBπa2μ0Iωcosωt2bRCπb2μ0Iωsinωt2aRDπb2μ0Iωcosωt2aR
A very small circular loop of radius a is initially (at t = 0) coplanar and concentric with a much larger fixed circular loop of radius b. A constant current I flows in the larger loop. The smaller loop is rotated with a constant angular speed ω about the common diameter. The emf induced in the smaller loop as a function of time t is
View SolutionA very small circular loop of radius a is initially (at t = 0) coplanar and concentric with a much larger fixed circular loop of radius b. A constant current I flows in the larger loop. The smaller loop is rotated with a constant angular speed ω about the common diameter. The emf induced in the smaller loop as a function of time t is
View SolutionA very small circular loop of radius r is initially coplanar and concentric with a much larger circular loop of radius R(>>r) . A constant current i is passed in the larger loop which is kept fixed in space and the small loop is rotated with angular velocity ω about a diameter. The resistance of the small loop is R0 and the inductance is negligible.
(a) Find the current in the small loop as a function of time.
(b) Calculate how much troque must be exerted on the small loop to rotate it.
View SolutionA very small circular loop of radius a is initially coplanar & concentric with a much larger circular loop of radius b(<<a).A constant current I is passed in the large loop which is kept fixed in space & the small loop is rotated with constant angular velocity ω about a diameter.The resistance of the small loop is R & its inductance is negligible The induced emf in the large loop due to current induced in smaller loop as a function of time is equal to 1x(πa2μ0ωb)2Icos2ωtR.Find out value of x.
View SolutionA very small circular loop of radius a is initially coplanar & concentric with a much larger circular loop of radius b (>>a). A constant current is passed in the large loop which is kept fixed in space & the small loop is rotated with angular velocity omega about a diameter. The resistance of the small loop is R & its self inductance is negligible. The current in the larger loop is clockwise.
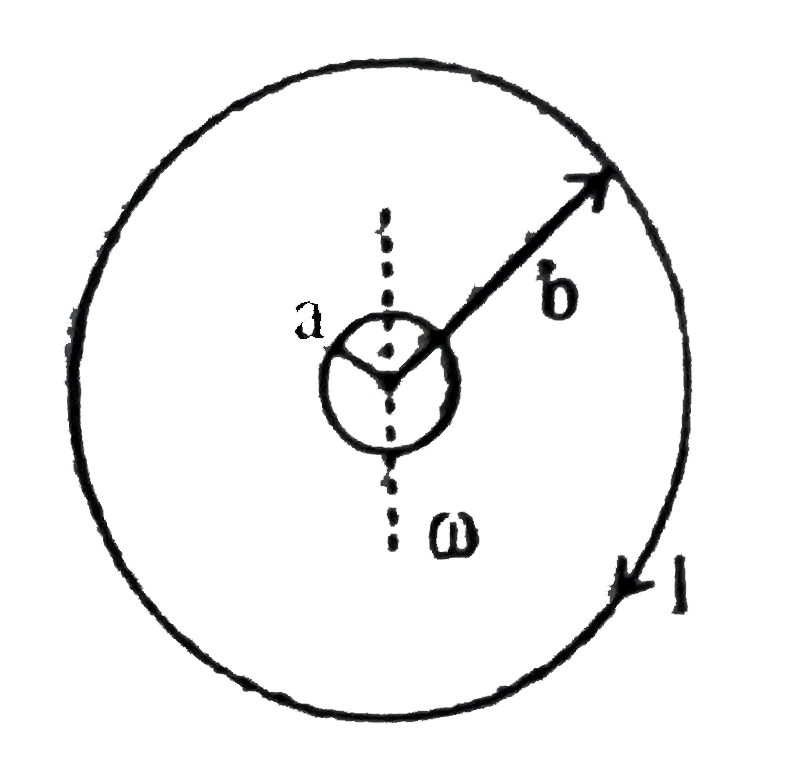
At the moment both the loops are in the same plane
View Solution
