कथन यदि C1,C2 तथा C3 धारिता के तीन संधारित्रों को समान्तर क्रम तथा श्रेणीक्रम में संयोजित किया गया है, तब CP>Ca
कारण 1CP=1C1+1C2+1C3
कथन और कारण दोनों सत्य हैं तथा कारण कथन की सत्य व्याख्या करता है।
कथन और कारण दोनों सत्य हैं लेकिन कारण, कथन की सत्य व्याख्या नहीं करता है।
कथन सत्य है, लेकिन कारण असत्य है।
कथन और कारण दोनों असत्य हैं।
The correct Answer is:C
कथन सत्य है , क्योंकि समांतर क्रम में धारिता श्रेणीक्रम संयोजन से अधिक होगी। कारण असत्य है क्योंकि
Cp=C1+C2+C3
Topper's Solved these Questions
- स्थिरवैद्युत विभव तथा धारिता BOOK - NEET PREVIOUS YEARCHAPTER - स्थिरवैद्युत विभव तथा धारिता EXERCISE - NCERT व NCERT Exemplar के प्रश्न
17 Videos
- स्थिरवैद्युत विभव तथा धारिता BOOK - NEET PREVIOUS YEARCHAPTER - स्थिरवैद्युत विभव तथा धारिता EXERCISE - NCERT पर BASED OBJECTIVE प्रश्न (स्थिरवैद्युत स्थितिज ऊर्जा )
65 Videos
- स्थिर वैद्युत विभव तथा धारिताBOOK - NEET PREVIOUS YEARCHAPTER - स्थिर वैद्युत विभव तथा धारिताEXERCISE - MCQs
27 Videos
Similar Questions
5×10−8C तथा −3×10−5C के दो आवेश 16 सेमि की दुरी पर स्थित है। दोनों आवेशों को मिलाने वाली रेखा के किस बिंदु पर विभव शून्य है? अंतर पर विभव शून्य लीजिए।
View Solution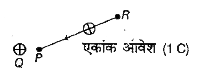
बिंदु R तथा P के मध्य स्थितिज ऊर्जा का अंतर है
View Solutionकिसी संधारित्र को एक बैटरी से आवेशित किया जाता है फिर बैटरी को हटाकर, इस संधारित्र से, समान्तर क्रम मे ठीक ऐसा ही एक अन्य अनावेशित संधारित्र जोड़ दिया जाता है, तो इस प्रकार बने परिणामी निकाय की कुल स्थिर वैधुत ऊर्जा (पहले संधारित्र की तुलना मे )
View SolutionIIf y=1+c_1/(x-c_1)+(c_2x)/((x-c_1)(x-c_2))+(c_3 x^2)/((x-c_1)(x-c_2)(x-c_3)) show that dy/dx=(y/x)[c_1/(c_1-x)+c_2/(c_2-x)+c_3/(c_3-x)]
View Solution∣∣ ∣ ∣∣111nc1n+1c1n+2c1n+1c2n+2c2n+3c2∣∣ ∣ ∣∣=1
View SolutionC1C0+2.C2C1+3.C3C2+….+n.CnCn−1=
View SolutionC0C1+C1C2+C2C3+…+Cn−1Cn=
View SolutionI : C1C2+2C2C1+3.C3C2+…...+n.CnCn−1=n(n+1)2
II : C0+C12+C23+….+Cnn+1=2n+1−1n+1
View Solution(1+c1c0)(1+c2c1)(1+c3c2)⋯(1+cncn−1)-এর মান হয়-
View SolutionIf C1,C2,C3,C4 are the coefficients of any consecutive terms in the expansion of (1+x)n , prove that :
C1C1+C2+C3C3+C4=2C2C2+C3
View SolutionProve that (C0+C1)(C1+C2)…..(Cn−1+Cn)=(n+1)nn!(C1.C2.C3……Cn)
View SolutionC0−[C1−2.C2+3.C3−……..+(−1)n−1.n.Cn] =
View Solution(C0+C1)(C1+C2)(C2+C3)………(Cn−1+Cn)C0C1C2…Cn
View SolutionThe value of ∣∣111nCn+21Cn+41Cn1Cn+22Cn+42C2∣∣ is
View SolutionShow that C0C1+C1C2+C2C3+....+Cn−1Cn
= 2n!(n−1)!(n+1!)
View SolutionProve that (C0+C1)(C1+C2)(C2+C3)...(Cn−1+Cn)=C0C1C2...Cn−1(n+1)nn!
View Solution
