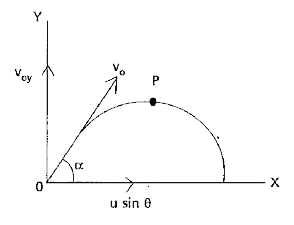
Shows that the projection angle θo for a projectile launched from the origin is given by θo=tan−1(4hmR) where the symbols have their usual meaning.Solution in Punjabi
Step by step video & image solution for Shows that the projection angle theta_o for a projectile launched from the origin is given by theta_o=tan^-1((4h_m)/R) where the symbols have their usual meaning. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
Similar Questions
Is it necessary to mention the direction of a vector having zero magnitude?
02:35View SolutionName the device used for measuring the mass of atoms and molecules.
05:18View SolutionIn which of the following examples of motion, can the body be considered approximately a point object:
04:18View SolutionShow that projection angle θ0 for a projectile launched from the origin is given by:
θ0=tan−1[4HmR] Where Hm= Maximum height, R=RangeView Solutionसिद्ध कीजिये की मूल बिंदु से फेंके एक गए प्रक्षेप्य कोण का मान tan−1(4hmR) होंगे | यहां प्रयुक्त प्रतीकों के अर्थ सामान्य है |
05:35View SolutionShow that the projection angle theta_0 for a projectile launched from the origin is given by theta_0=tan^(-1)((4H)/R) Where the symbols have their usual meaning.
07:48View Solution(a) Show that for a projectile the angle between the velocity and the X-axis as a function of time is given by
θ(t)=tan−1[voy−gtvox]
(b) Show that the projection angle θ0 for a projectile lunched from the origin is given by θ0=tan−1(4hmR),
where the symbols have their usual meanings .02:39View Solution(a) Show that for a projectile the angle between the velocity and the x - axis as a function of time is given by
θ(t)=tan−1(v0y−gtv∘x)
(b) Shows that the projection angle θ∘ for a projectile launched from the origin given by
θ0=tan−1(4hmR)
where the symbols have their usual meaning.05:08View Solution(a) Show that for a projectile the angle between the velocity and the x - axis as a function of time is given by
θ(t)=tan−1(v0y−gtv∘x)
(b) Shows that the projection angle θ∘ for a projectile launched from the origin given by
θ0=tan−1(4hmR)
where the symbols have their usual meaning.05:23View Solution(a) Show that for a projectile the angle between the velocity and the x - axis as a function of time is given by
θ(t)=tan−1(v0y−gtv∘x)
(b) Shows that the projection angle θ∘ for a projectile launched from the origin given by
θ0=tan−1(4hmR)
where the symbols have their usual meaning.04:02View SolutionShow that for a projectile the angle between the velocity and the x-axis as function of time is given
by θt=tan−1(v0y−gtvox)
(b) Shows that the projection angle θ0 for a projectile launched from the origin is given by θt=tan−1(4hmR)
where the symbols have their usual meanings.02:59View SolutionProve that, projectile from the origin theta_(0) Projection angle when projected at projection angle theta_(0)=tan^(-1)[(4H_(m))/(R)] it happens. Where H_(m) = Maximum height, R = Horizontal range
02:42View SolutionShow that a + r +1=1 where symbols have their usual meaning.
View SolutionShow that projection angle θ0 for a projectile launched from the origin is given by:
θ0=tan−1[4HmR] Where Hm= Maximum height, R=Range03:26View SolutionShows that the projection angle theta_o for a projectile launched from the origin is given by theta_o=tan^-1((4h_m)/R) where the symbols have their usual meaning.
02:04View SolutionShow that the projection angle θ for a projectile launched from the origin is given y θ(t)=tan−1[υ∘0y−gtυ0x]
θ0=tan−1(4hmR) where the symbols have their usual meaning.
 06:22View Solution
06:22View Solution

