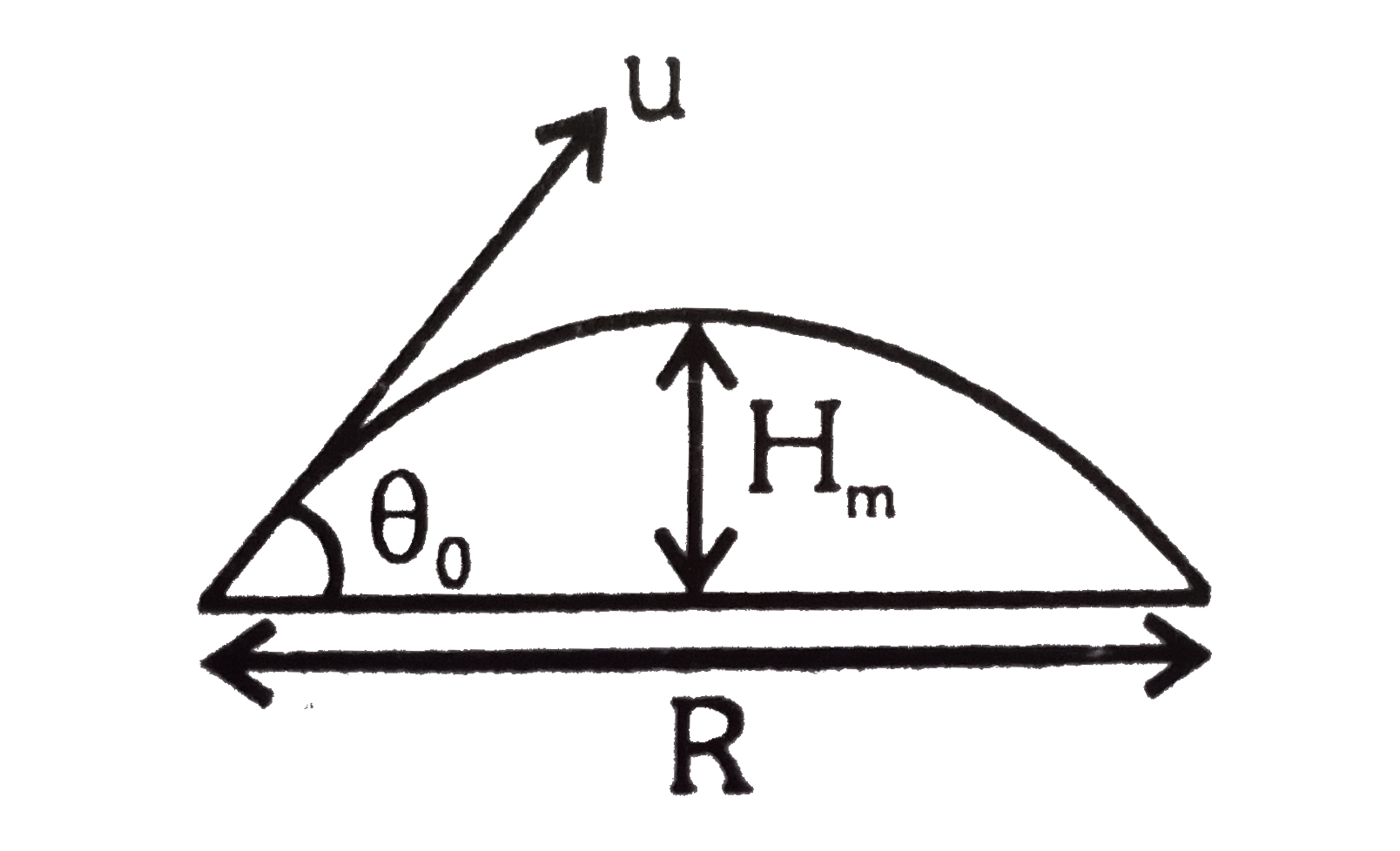
Show that projection angle θ0 for a projectile launched from the origin is given by:
θ0=tan−1[4HmR] Where Hm= Maximum height, R=RangeSolution in Gujrati
Hm=u2sin2θ02g and R=2u2g×sinθ0×cosθ0
So, HmR=tanθ04⇒tanθ0=4HmR⇒=tan−1(4HmR)
Topper's Solved these Questions
Similar Questions
Assertion : A body can have acceleration even if its velocity is zero at a given instant of time.
Reason : A body is momentarily at rest when it reverses its direction of motion.
View SolutionA particle is moving in xy-plane .At certain instant the components of its velocity and acceleration are as follows ux=3m/s,uy=4m/s,ax=2m/s2anday=1m/s2. The rate of change of speed at this moment is
View SolutionA piece of wire is bent in the shape of a parabola y=kx2 (y-axis vertical) with a bead of mass m on it. The bead can slide on the wire without friction. It stays at the lowest point of the parabola when the wire is at rest. The wire is now accelerated parallel to the x-axis with a constant acceleration a. The distance of the new equilibrium position of the bead, where the bead can stay at rest with respect to the wire, from the y-axis is:
View SolutionShow that projection angle θ0 for a projectile launched from the origin is given by:
θ0=tan−1[4HmR] Where Hm= Maximum height, R=Range
View SolutionFind the ratio of maximum horizontal range and the maximum height attained by the projectile. i.e. for theta_(0) = 45^(@)
View SolutionA body is projected at an angle theta with the horizontal. Derive an expression for its horizontal range. Show that there are two angles theta_(1) and theta_(2) projections for the same horizontal range, such that theta_(1)+theta_(2)=90^(@) .
View SolutionThe distance of the roots of the equation tanθ0zn+tanθ1zn−1+…+tanθn=3 from z=0, where θ0,θ1,θ2,…,θn∈[0,π4] satisfy
View SolutionShow that the projection angle theta_0 for a projectile launched from the origin is given by theta_0=tan^(-1)((4H)/R) Where the symbols have their usual meaning.
View Solution(a) Show that for a projectile the angle between the velocity and the X-axis as a function of time is given by
θ(t)=tan−1[voy−gtvox]
(b) Show that the projection angle θ0 for a projectile lunched from the origin is given by θ0=tan−1(4hmR),
where the symbols have their usual meanings .
View SolutionA particle is projected with velocity u at angle θ1 with horizontal .The ratio of range and maximum height is 4. When it is projected at angle θ2 with horizontal with same speed,the ratio of range and maximum height is 2.Then tanθ1tanθ2 will be equal to
View SolutionA projectile's launch speed is 6.00 times that of its speed at its maximum height. Find the launch angle theta_(0) .
View Solution(a) Show that for a projectile the angle between the velocity and the x - axis as a function of time is given by
θ(t)=tan−1(v0y−gtv∘x)
(b) Shows that the projection angle θ∘ for a projectile launched from the origin given by
θ0=tan−1(4hmR)
where the symbols have their usual meaning.
View Solution(a) Show that for a projectile the angle between the velocity and the x - axis as a function of time is given by
θ(t)=tan−1(v0y−gtv∘x)
(b) Shows that the projection angle θ∘ for a projectile launched from the origin given by
θ0=tan−1(4hmR)
where the symbols have their usual meaning.
View Solution(a) Show that for a projectile the angle between the velocity and the x - axis as a function of time is given by
θ(t)=tan−1(v0y−gtv∘x)
(b) Shows that the projection angle θ∘ for a projectile launched from the origin given by
θ0=tan−1(4hmR)
where the symbols have their usual meaning.
View SolutionShow that for a projectile the angle between the velocity and the x-axis as function of time is given
by θt=tan−1(v0y−gtvox)
(b) Shows that the projection angle θ0 for a projectile launched from the origin is given by θt=tan−1(4hmR)
where the symbols have their usual meanings.
View SolutionProve that, projectile from the origin theta_(0) Projection angle when projected at projection angle theta_(0)=tan^(-1)[(4H_(m))/(R)] it happens. Where H_(m) = Maximum height, R = Horizontal range
View Solution
