AB is the diameter of a semi-circle. Through A draw any straight lines AP, AQ meet the circumference again at P and Q. Draw PM, QN perpendicular to AB. Then the ratio AM:AN is equal to
(A) BP2:BQ2
(B) AP2:AQ2
(C) AP2:BQ2
(D) none of these
Step by step video solution for AB is the diameter of a semi-circle. Through A draw any straight lines AP, AQ meet the circumference again at P and Q. Draw PM, QN perpendicular to AB. Then the ratio AM:AN is equal to (A) BP^2:BQ^2 (B) AP^2: AQ^2 (C) AP^2:BQ^2 (D) none of these by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Similar Questions
AB is the diameter of a semi-circle. Through A draw any straight lines AP, AQ meet the circumference again at P and Q. Draw PM, QN perpendicular to AB. Then the ratio AM:AN is equal to
(A) BP2:BQ2
(B) AP2:AQ2
(C) AP2:BQ2
(D) none of these
View SolutionDraw a line segment AB=6.2 cm. mark a point P in AB such that BP=4 cm. through point P draw a perpendicular to AB.
View Solution
Knowledge Check
ABCD is a rhombus. A line passing through C cuts extended line AD and AB at Q and P respectively. If QD=12AB. Then find the ratio AB to PB.
 A2:1B1:2C1:1D3:1
A2:1B1:2C1:1D3:1Let a1,a2,a3 …..be in A.P. and ap,aq,ar be in G.P. Then aq:ap is equal to :
Ar−pq−pBq−pr−qCr−qq−pD1
If a line is drawn through a point A(3,4) to cut the circle x2+y2=4 at P and Q then AP .AQ=
View SolutionIn a circle of radius 3 units, a diameter AB intersects a chord of length 2 units perpendicularly at P. If AP>BP, then what is the ratio of AP to BP?
View SolutionIn a circle of radius 2 units, a diameter AB intersects a chord of length 2 units perpendicularly at P. If AP>BP, then AP is equal to
View SolutionDraw AB = 9.7 cm. Take a point P on it such that A - P - B and AP = 3.5 cm. Through P draw a line perpendicular to seg AB.
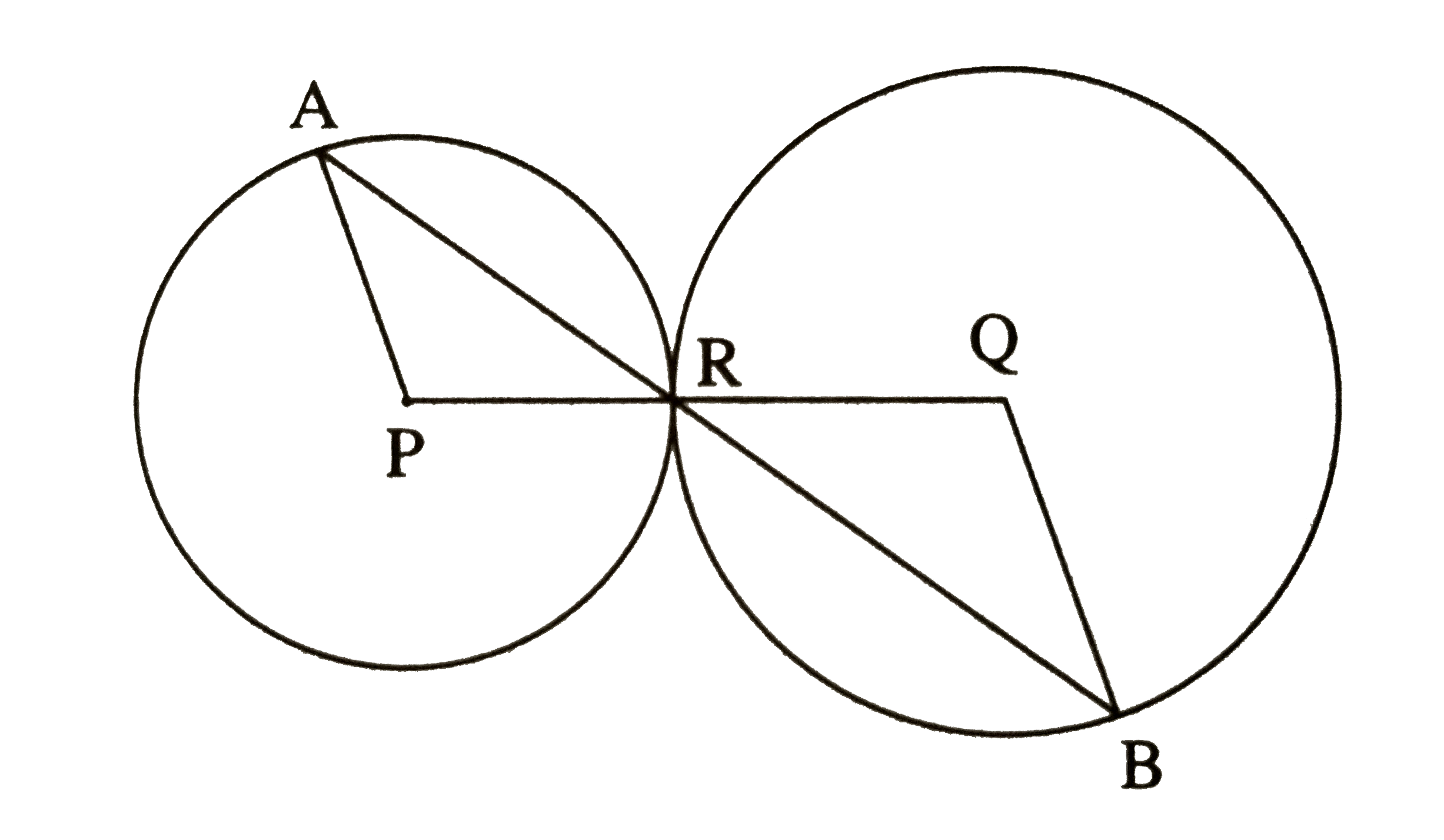
View SolutionIn the figure, the circles with centers P and Q touch each other at R.A line passing through R meets the circles at A and B respectively. Prove that
seg AP || seg BQ
View SolutionLet a1,a2,a3 …..be in A.P. and ap,aq,ar be in G.P. Then aq:ap is equal to :
View Solution
