Find all values of the parameter a for which the inequality $a {.9}^{x} + 4 (a - 1) 3^{x} + a > 1$ is satisfied for all real values of xSolution in Gujrati

Video Solution

Text Solution

Verified by Experts

Putting $t = 3^{x}$ in the original equation then we obtain

$a t^{2} + 4 (a - 1) t + a > 1$
$\Rightarrow a t^{2} + 4 (a - 1) t + (a - 1) > 0 [t > 0, ∵ 3^{x} > 0]$
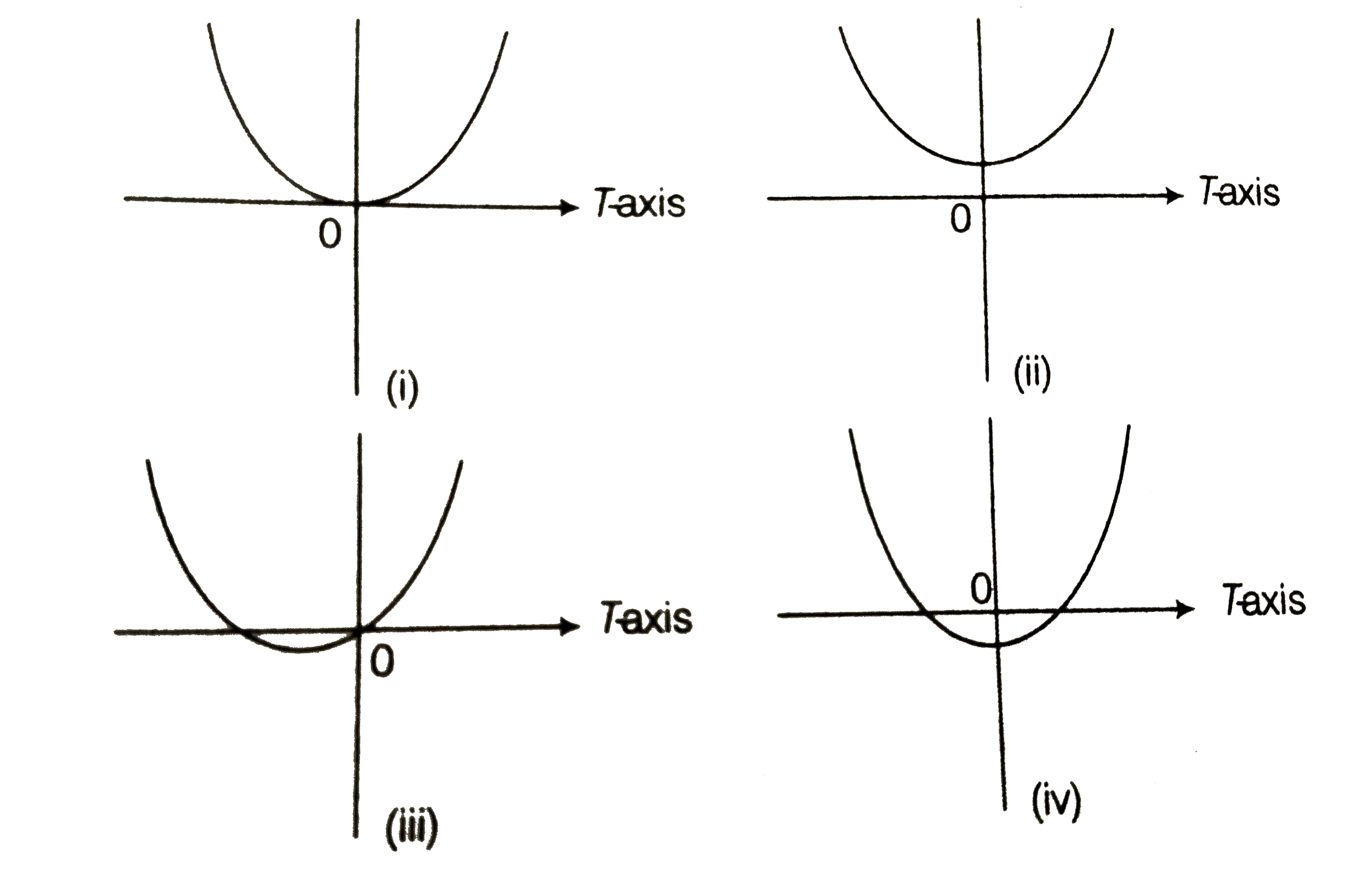
This is possible in two cases. First the parabola
$f (t) = a t^{2} + 4 (a - 1) t + (a - 1)$ opens upwards with its vertex(turning point) lying in the non-positive part of the T-axis, as shwon in the following four figures.
$∴ a > 0$ and sum of roots $\leq 0$
$\Rightarrow - \frac{4 (a - 1)}{2 a} \leq 0$ and $f (0) \geq 0$
$∴ a > 0, a - 1 \geq 0$ and $a - 1 \geq 0$
Hence $a \geq 1$

Second the parabola $f (t)$ opens upward with its vertex lying in positive direction of $t$ then
$a > 0, \frac{4 (a - 1)}{2 a} > 0$ and $D \leq 0$
$\Rightarrow a > 0, (a - 1) < 0$
and $16 {(a - 1)}^{2} - 4 (a - 1) a \leq 0$
$\Rightarrow a > 0, a < 1$
an $4 (a - 1) (3 a - 4) \leq 0$
$\Rightarrow a > 0, a < 1$ and $1 \leq a \leq \frac{4}{3}$
These inequalities cannot have simultaneously.
Hence $a \geq 1$ from eq. i

Updated on:21/07/2023

|

Class 12 MATHS QUADRATIC EQUATIONS

Similar Questions

Recommended Questions

Home
Ask Doubt
Profile