for what values of m, the equation 2x2−2(2m+1)x+m(m+1)=0,m∈R has
(i) Both roots smallar than 2 ?
(ii) Both roots greater than 2 ?
(iii) Both roots lie in the interval (2,3) ?
(iv) Exactly one root lie in the interval (2,3) ?
(v) One root is smaller than 1, and the other root is greater than 1 ?
(vi) One root is greater than 3 and the other root is smaller than 2 ?
(vii) Roots αandβ are such that both 2 and 3 lie between αandβ ? Solution in Gujrati
The correct Answer is:(i) mεg(−∞,7−√32) (ii) mε(7+√332,∞) (iii) mεϕ
(iv) mε(7−√32,11−√732)∪(7+√332,11+√732)
(v) mε(0,3) (vi) mε(7−√32,7+√332)
(vii) mε(7−√332,11−√732)∪(7+√332,11+√732)
(viii) mε(7−√32,7+√332)∪(7+√32,∞)
(ix) mε(−∞,7−√332)∪((7−√332,7+√332)
(x) mε((11-sqrt(73))/2,(7+sqrt(3))/2)
∵2x2−2(2m+1)x+m(m+1)=0[∵mεR]
∴D=[−2(2m+1)]2−8m(m+1)[D=b2−4ac]
=4{(2m+1)2−2m(m+1)}
=4(2m2+2m+1)
=8(m2+m+12)=8{(m+12)2+14}>0
or D>0,∀mεolonR……i
x coordinate of vertex =−b2a=2(m+1)4=(m+12).....ii
and let
f(x)=x2−(2m+1)x+12m(m+1) ...........iii
(i) Both roots are smaller than 2.

Consider the following cases:
Case I D≥0
∴mεR [from Eq. (i) ]
CaseII x-coordinate of vertex <2.
⇒m+12<0 [from Eq. (ii) ]
or m<32
Case III f(2)>0
⇒4−(2m+1)2+12m(m+1)>0
⇒m2−7m+4>0
∴mε(−∞,7−√32)∪(7+√332,∞)
Combining all cases we get
mε(−∞,7−√32)
(ii) Both roots are greater than 2.
Consider the following cases.
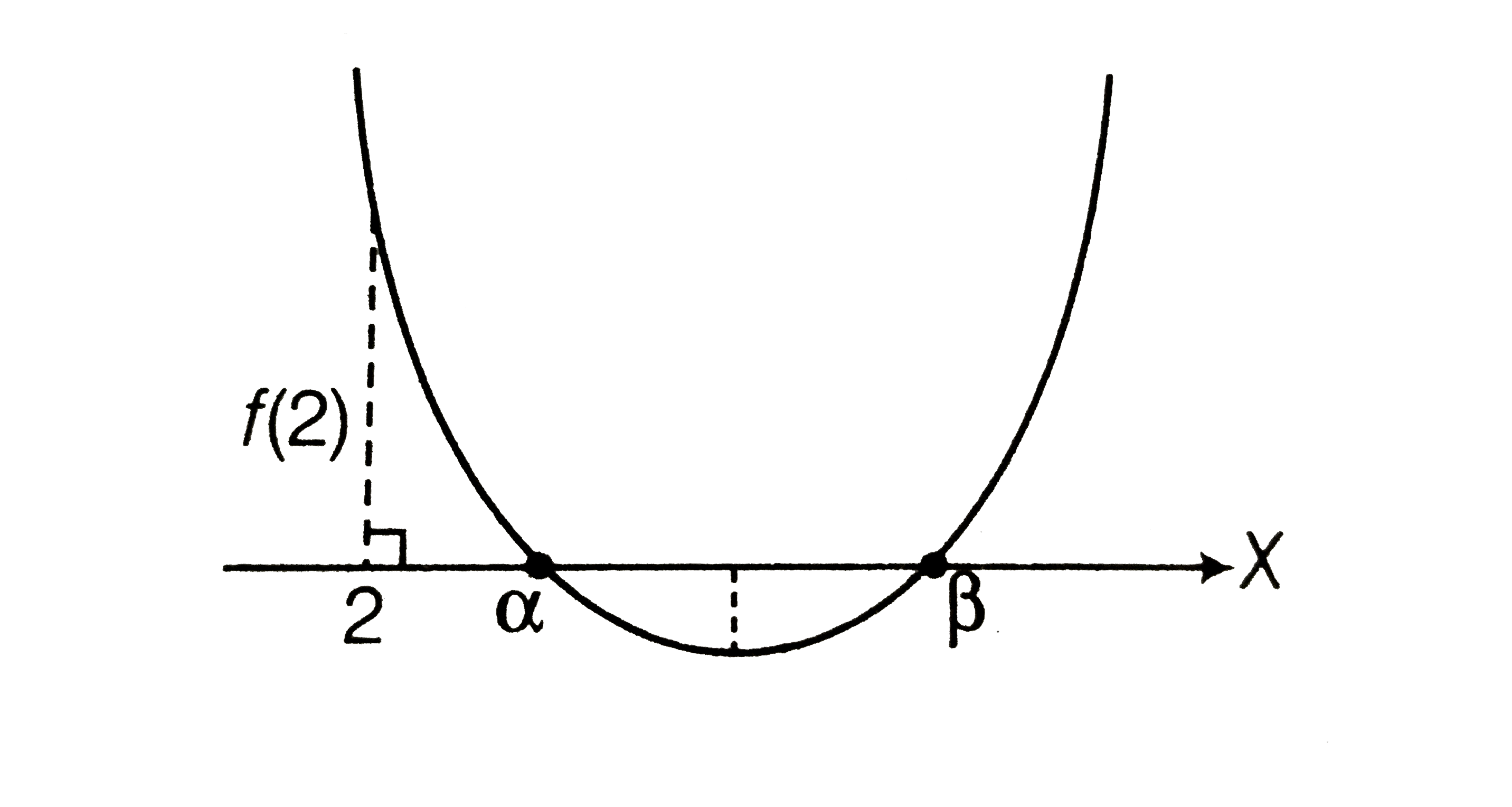
Case I D≥0
∴mεR[from Eq. (i)]
Case II x- coordinate of vertex >2
⇒m+12>2[ from Eq. (ii)]
∴m>32
Case III f(2)>0
mε(−∞,7−√332)∪(7+√332,∞) [from part (a) ]
Combining all cases, we get
mε(7+√332,∞)
(iii) Both roots lie in the interval (2,3).
Consider the following cases:

CAse I D≥0
∴mεR [from Eq. (i)]
Case II f(2)>0
∴mε(−∞,7−√32)∪(7+√332,∞) [from part (a)]
Case Case III f(3)>0
⇒9−3(2m+1)+12m(m+1)>0
or m2−11m+12>0
:mε(−∞,11−√732)∪(11+√732,∞)
Case IV 2<x -coordinate of vertex <3
⇒2<m+12<3
or 32<m<52 or mε(32,52)
Combining allcases we get
mεϕ
(iv) Exactly one root lie in the interval (2,3).
Consiser the following cases:
Case I D>0
∴mεR [from Eq (i) ]
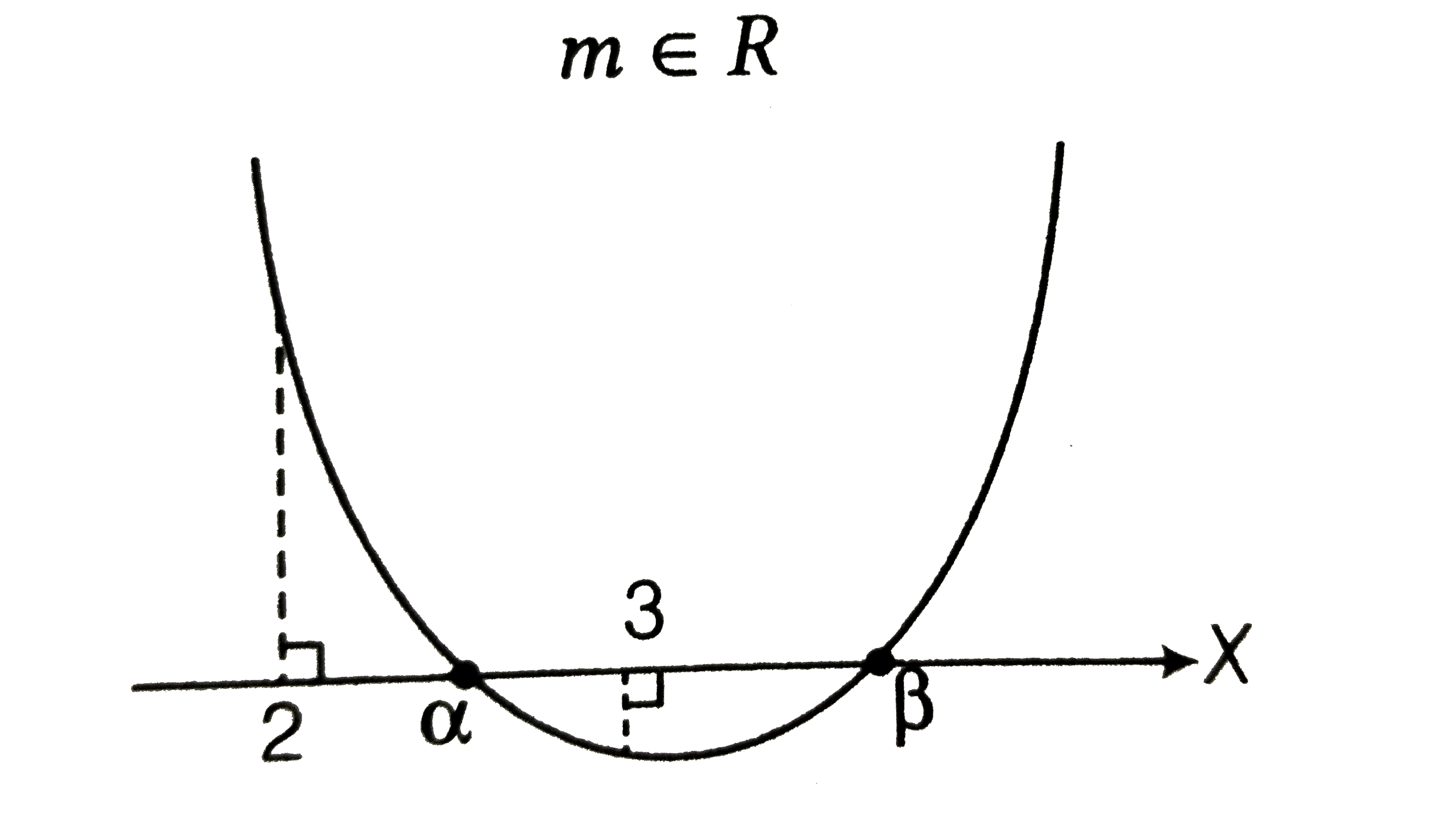
Case II f(2)f(3)<0
(4−2(2m+1)+12m(m+1))
(9−3(2m+1)+12m(m+1))<0
⇒(m2−7m+4)(m2−11m+12)<0
⇒(m−7−√332)(m−7+√332)
(m−11−√732)(m−11+√732)<0
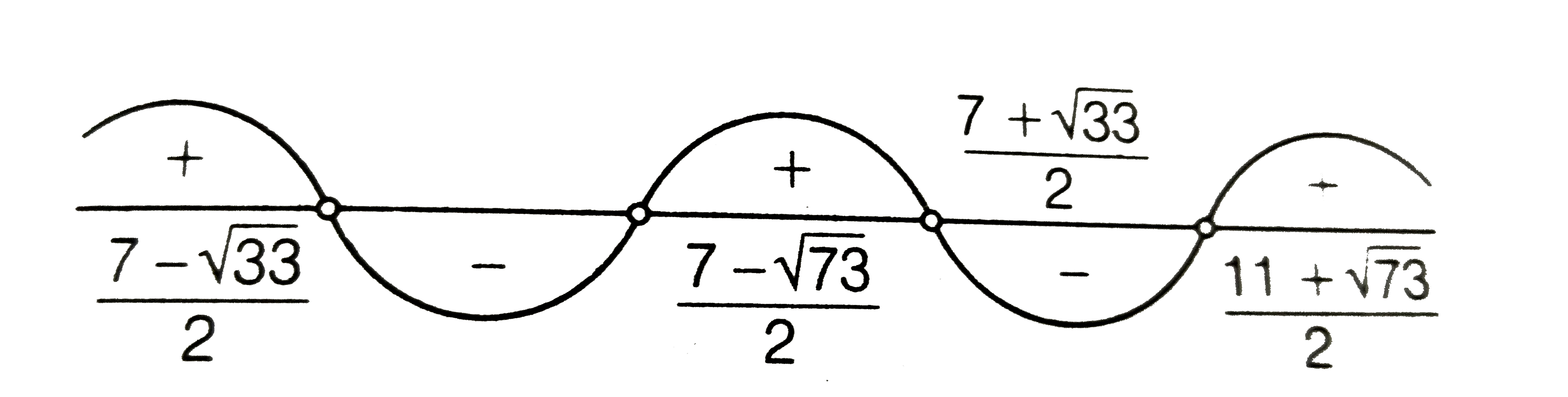
∴mε(7−√332,11−√332)∪(7+√332,11+√732)
Combining all cases we get
mε((7-sqrt(33))/2,(11-sqrt(73))/2))uu((7+sqrt(33))/2,(11+sqrt(73))/2)<br>(v)O≠i√ssmal≤rthan1andtheotheri√sgreaterthan1.<br>Consiserthefollow∈gcases.<br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/ARH_SKG_ALG_C02_E12_002_S06.pngwh=80%mx-autosty≤=background:white;><br>CaseIDgt0<br>:.m epsilonR[omEq.(i)]<br>CaseIIf(1)lt0<br>implies1-(2+1)+1/2m(m+1)lt0[omEq.(iii)]<br>impliesm^(2)-3mlt0<br>impliesm(m-3)lt0<br>:.m epsilon (0,3)<br>Comb∈∈g⊥hcaseswe≥t<br> m epsilon(0,3)<br>(vi)O≠i√sgreaterthan3andtheotheri√ssmal≤rthan2.<bR>Consiserthefollow∈gcases<br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/ARH_SKG_ALG_C02_E12_002_S07.pngwh=80%mx-autosty≤=background:white;><br>CaseIDgt0<br>:. m epsion R[omEq.(i)]<br>CaseIIf(2)lt0<br>impliesm^(2)-8m+4lt0<br>:.(7-sqrt(33))/2ltmlt(7+sqrt(33))/2<br>:. m epsilon ((7-sqrt(33))/2ltm lt (7+sqrt(33))/2<br>:. M epsilon ((7-sqrt(33))/2,(7+sqrt(33))/2)<br>CaseIIIf(3)lt0<br>impliesm^(2)-11m+12lt0<br>:.(11-sqrt(73))/2ltmlt (11+sqrt(73))/2<br>:. m epsilon ((11-sqrt(73))/2, (11+sqrt(73))/2)<br>Comb∈∈gallcaseswe≥t<br>m epsilon ((7-sqrt(33))/2, (7+sqrt(33))/2)<br>(vii)At≤∗o≠l√ies∈the∫erval(2,3).<br>i.e.(d)uu(c)<br>:.mepsilon((7-sqrt(33))/2,(11-sqrt(73))/2)uu((7+sqrt(33))/2,(11+sqrt(73))/2)<br>(viii)At≤∗o≠i√sgreaterthan2.<br>i.e(Exactlyo≠i√sgreaterthan2)uu(Boths√aregreater2).<br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/ARH_SKG_ALG_C02_E12_002_S08.pngwh=80%mx-autosty≤=background:white;><br>of(Exactlyo≠i√sgreaterthan2)uu(b)…..i<br>Consrthefollow∈gcases:<br>CaseIDgt0<br>:. m epsilon[omEq.(i)]<br>CaseIIf(2)lt0<br>impliesm^(2)-7m+4lt0<br>:.m epsilon ((7-sqrt(33))/2,(7+sqrt(33))/2)<br>Comb∈∈g⊥hcaseswe≥t<br>m epsilon ((7-sqrt(33))/2,(7+sqrt(33))/2)………ii<br>F∈allyomEqsiandiiwe≥t<br> m epsilon ((7-sqrt(33))/2,(7+sqrt(33))/2)uu((7+sqrt(33))/2,oo)<br>(ix)At≤∗o≠i√ssmal≤rthan2.<br>i.e(Exactlyo≠i√ssmal≤rthen2)uu(Boths√aresmal≤rthan2)<br>or(h)IIuu(a)<br>We≥tm epsilon (-oo,(7-sqrt(33))/2)uu((7-sqrt(33))/2,(7+sqrt(33))/2)<br>(x)Both2and3liebetweenalphaandbeta<br>Consrthefollow∈gcases:<br>CaseDgt0<br>:. mepsilonR[omEq(i)]<br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/ARH_SKG_ALG_C02_E12_002_S09.pngwh=80%mx-autosty≤=background:white;><br>CaseIIf(2)lt0<br>impliesm^(2)-7m+4lt0<br>:. m epsilon ((7-sqrt(33))/2,(7+sqrt(33))/2)<br>CaseIIIf(3)lt0<br>impliesm^(2)-11m+12lt0<br>:.m epsilon((11-sqrt(73))/2,(11+sqrt(73))/2)<br>Comb∈∈gallcaseswe≥t<br>m epsilon ((11-sqrt(73))/2,(7+sqrt(33))/2)
Similar Questions
Let x2−(m−3)x+m=0(mεR) be a quadratic equation . Find the values of m for which the roots are (ix)one root is smaller than 2 & other root is greater than 2 (x) both the roots are greater than 2 (xi) both the roots are smaller than 2 (xii)exactly one root lies in the interval (1;2) (xiii) both the roots lies in the interval (1;2) (xiv) atleast one root lies in the interval (1;2) (xv) one root is greater than 2 and the other root is smaller than 1
View SolutionFor what values of m the equation (1+m)x2−2(1+3m)x+(1+8m)=0 has (m∈R)
(i) both roots are imaginary?
(ii) both roots are equal?
(iii) both roots are real and distinct?
(iv) both roots are positive?
(v) both roots are negative?
(vi) roots are opposite in sign?
(vii)roots are equal in magnitude but opposite in sign?
(viii) atleast one root is positive?
(iv) atleast one root is negative?
(x) roots are in the ratio 2:3?
View Solutionf(x)=x2−(m−3)x+m=0 is a quadratic equation, find values of m for which
both roots lie in the interval [2,3]
View SolutionLet x2−(m−3)x+m=0(m∈R) be a quadratic equation, then find the values of 'm' for which both
(a) the roots are greater than 2.
(b) both roots are positive,
( c) one root is positive and other is negative.
( d) One root is greater than 2 and other smaller than 1
( e) Roots are equal in magnitude and opposite in sign,
( f) both roots lie in the interval (1, 2)
View SolutionIf both the roots of the equation 4x2−2x+m=0 lie in the interval (−1,1), then
View SolutionLet x2−(m−3)x+m=0(m∈R) be a quadratic equation . Find the values of m for which the roots are:
(ix)one root is smaller than 2 & other root is greater than 2
(x) both the roots are greater than 2.
(xi) both the roots are smaller than 2.
(xii) exactly one root lies in the interval (1,2)
(xiii) both the roots lies in the interval (1,2)
(xiv) at least one root lies in the interval (1,2)
(xv) one root is greater than 2 and the other root is smaller than 1
View SolutionFor what values of m the equation (1+m)x2−2(1+3m)x+(1+8m)=0 has (m∈R)
(i) both roots are imaginary?
(ii) both roots are equal?
(iii) both roots are real and distinct?
(iv) both roots are positive?
(v) both roots are negative?
(vi) roots are opposite in sign?
(vii)roots are equal in magnitude but opposite in sign?
(viii) atleast one root is positive?
(ix) atleast one root is negative?
(x) roots are in the ratio 2:3?
View Solution
