If A, B are two sets, prove that A∪B=(A−B)∪(B−A)∪(A∩B).
and prove that
n(A∪B)=n(A)+n(B)−n(A∩B)
where, n(A) denotes the number of elements in A. Solution in Gujrati
Video Solution
Text Solution
Let x∈A∪B⇒x∈Aorx∈B
iff(x inAandxcancelinB)or(x inBandxcancelinA)
or (x∈Aandx∈B) [from definition of union]
⇔x∈(A−B)orx∈(B−A)orx∈A∩B
⇔x∈(A−B)∪(B−A)∪(A∩B)
∴A∪B⊆(A−B)∪(B−A)∪(A∩B)
and (A−B)∪(B−A)∪(A∩B)⊆A∪B
Hence, A∪B=(A−B)∪(B−A)∪(A∩B)
Let the common elements in A and B are z and only element of A are x (represented by vertical lines in the Venn diagram) and only element of B are y (represented by horizontal lines in the Venn diagram)
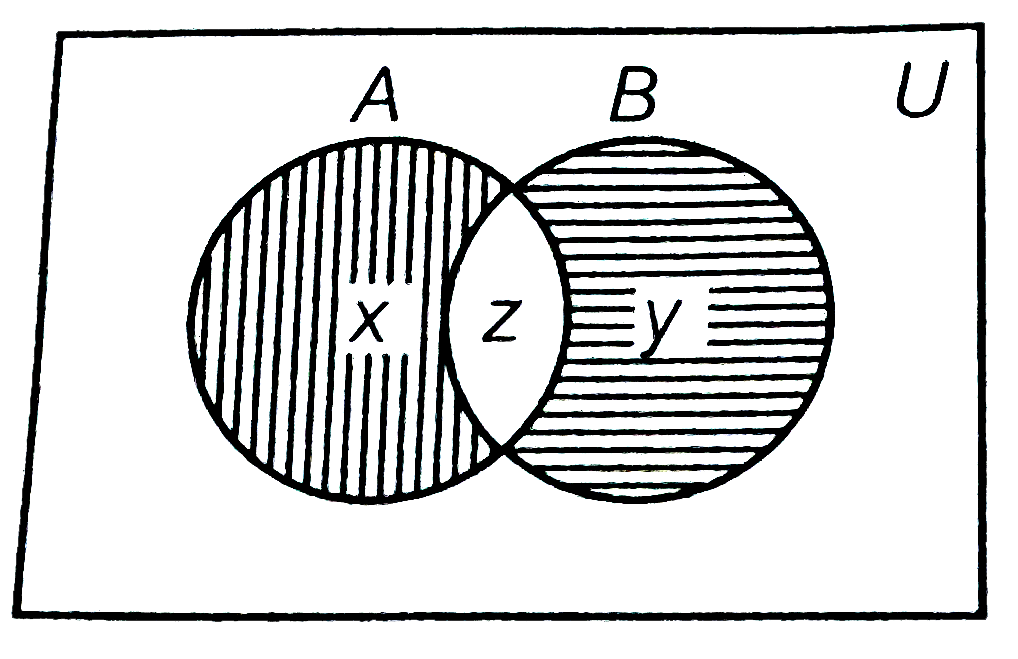
∴n(A) = Total elements of A = x + z
n(B) = Total elements of B = y + z
n(A∩B) = Common elements in A and B = z
Now, n(A∪B) = Total elements in complete region of A and B
x + y + z
=(x+z)+(y+z)−z
=n(A)+n(B)−n(A∩B)
Hence, n(A∪B)=n(A)+n(B)−n(A∩B)
|
Similar Questions
Establish that:n(A∪B)=n(A)+n(B)−n(A∩B)
View SolutionIf A and B are two sets such that n(A∪B)=50,n(A)=28,n(B)=32,then find n(A∩B).
View SolutionIf A, B are two sets, prove that A∪B=(A−B)∪(B−A)∪(A∩B).
Hence or otherwise prove that
n(A∪B)=n(A)+n(B)−n(A∩B)
where, n(A) denotes the number of elements in A.
View SolutionA and B are two sets. If n(A) = 17, n(B) = 23, and n(A∪B) = 38 find n(A∩B).
View SolutionIf A and B are two sets and n(A) = 15, n(B) = 25 and n(A∩B)=10 find n(A∪B)
View SolutionIf AandB are two sets, then (A−B)∪(A∩B) is equal to
(a) A∪B (b) A∩B (c) A (d) B
View SolutionIf A, B are two sets, prove that A∪B=(A−B)∪(B−A)∪(A∩B).
Hence or otherwise prove that
n(A∪B)=n(A)+n(B)−n(A∩B)
where, n(A) denotes the number of elements in A.
View Solution