Let A = {x, y, z), B = {u, v, w} and f : A → B be defined by f(x) = u,
f(y) = v, f(z) = w. Then, f is Solution in Gujrati
surjective but not injective
injective but not surjective
bijective
None of the above
The correct Answer is:C
A = {x, y, z}, B = {u, v, w}
Now, f : A→B
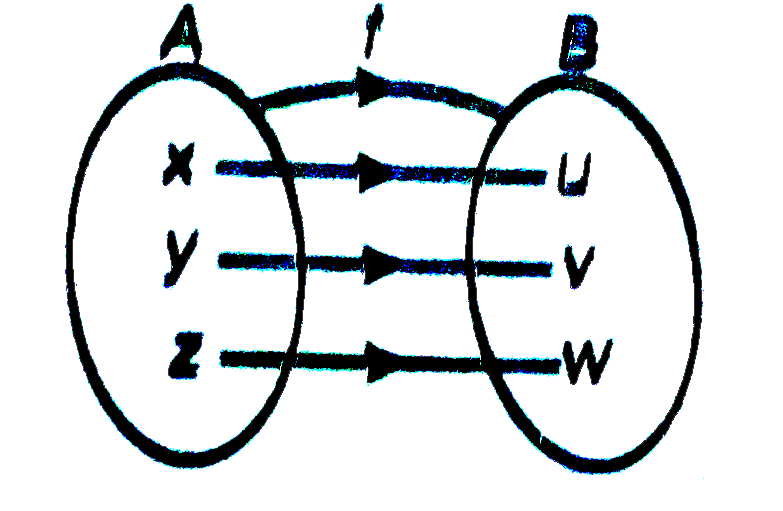
f is one-one and f is onto.
Similar Questions
दिया हुआ है कि A={x,y,z},B={u,v,w}, तो फलन f:A→B ताकि f(x)=u,f(y)=v,f(z)=v किस प्रकार का फलन होगा ?
View Solutionयदि A = {a, b, c}, B = {u, v, w} यदि f:A→B तथा g:B→A निम्न प्रकार परिभाषित हों कि
f= {(a, v), (b, u), (c, w)}
g= {(u, b), (v, a), (w,c)} तो (fog) ज्ञात कीजिए।
View Solutionयदि A = {a,b,c}, B = {u,v,w}
यदि f:A→Bतथा g:B→A निम्न प्रकार से परिभाषित हो
f={(a,v),(b,u),(c,w)}
g={(u,b),(v,a),(w,c)}
तो (fog) तथा (gof) ज्ञात कीजिए
View Solutionयदि A={a,b,c},B={u,v,w}
यदि f:A→B निम्न प्रकार g:B→A परिभाषित हो
f={(a,v),(b,u),(c,w)}
g{(u,b),(v,a),(w,c)} तो (fog) तथा (gof) ज्ञात कीजिए।
View SolutionLet A={u,v,w,x} .A bijective function f:A→A is chosen at random, then the probability that f(u)≠u,f(v)≠v,f(w)≠w and f(x)≠x is
1) 38
2) 1124
3) 164
4) 724
View SolutionLet A={u,v,w,x}. A bijective function f:A→A is chosen at random, then the probability that f(u)≠u,f(v)≠v,f(w)≠w and f(x)≠x is
View SolutionW (x,y,z) = xy + yz , x = u - v ,y = uv , z = u +v,u,v in R. Find ∂w∂u,∂w∂v and evaluate them at (12,1)
View SolutionLet A={a, b, c} , B={u v, w} and let f and g be two functions from A to B and from B to A respectively defined as: f={(a, v), (b, u), (c, w)} , g={(u, b), (v, a), (w, c)}. Show that f and g both are bijections and find fog and gof.
View Solution
