if D,E and F are the mid-points of the sides BC,CA and AB respectively of the ΔABCandO be any points, then prove that OA+OB+OC=OD+OE+OFSolution in Gujrati
Since, D is the mid-point of Bc, therefore by section formula, we have
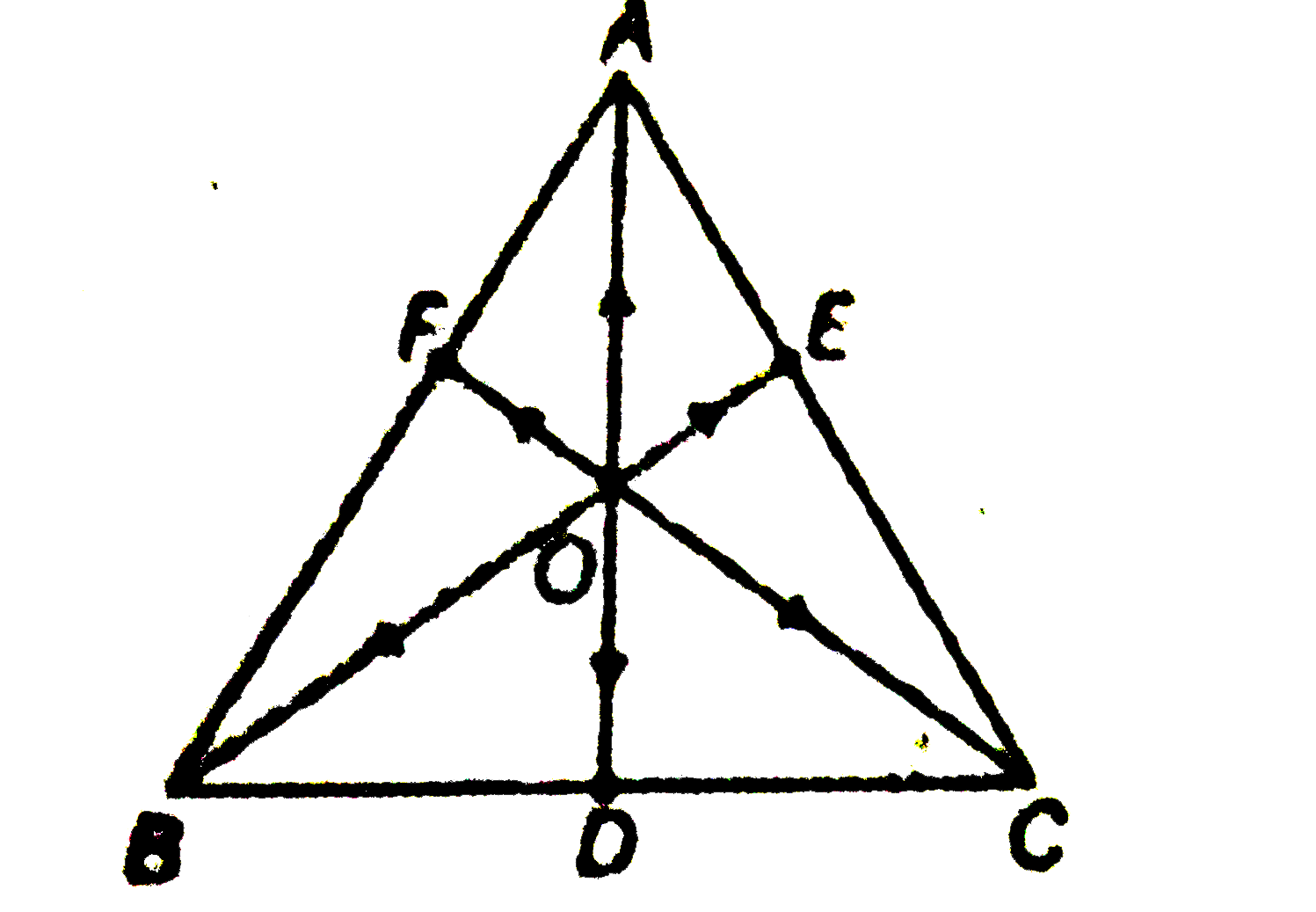
OD=OB+OC2
⇒OB+OC=2OD . . . (i)
Similarly, OC+OA=2OE . . (ii)
and OB+OA=2OF . . . (iii)
On adding Eqs. (i), (ii) and (iii), we get
2(OA+OB+OC)=2(OD+OE+OF)
⇒OA+OB+OC=OD+OE+OF Hence proved.
Similar Questions
ABCD is a quadrilateral and E is the point of intersection of the lines joining the mid-points of opposite sides. If O be any point in the plane, then show that −−→OA+−−→OB+−−→OC+−−→OD=4−−→OE.
View SolutionD, E and F are respectively the mid-points of sides AB, BC and CA of ΔABC. Find the ratio of the areas of ΔDEF and ΔABC.
View SolutionD and E respectively DeltaABC The side of AB is the mid-point of AB and AC and O is any point on the side BC. O is mixed with A. If P and Q are midpoints of OB and OC respectively, then DEQP is a
View SolutionO is any point in the exterior of a ΔABC. Prove that 2(OA+OB+OC)>(AB+BC+CA)
 .
.
View SolutionDand E are the mid-points of the sides AB and AC of ΔABC and O is any point on side BC. O is joined to A. If P and Q are the mid-points of OB and OC respectively, then DEQP is
View SolutionA point O lies inside a ΔABC. Show that OA+OB+OC>12(AB+BC+CA).
View SolutionIf D,E and F are the mid-points of the sides BC,CA and AB, respectively of a ΔABC and O is any point, show that
(i) AD+BE+CF=0
(ii) OE+OF+DO=OA
View SolutionD, E and F are the mid-points of the sides AB, BC and CA respectively of A ABC. AE meets DF at O. P and Q are the mid-points of OB and OC respectively. Prove that DPOF is a parallelogram.
View Solution
