P is a point on the side BC off the ΔABC and Q is a point such that PQ is the resultant of AP,PB and PC. Then, ABQC is aSolution in Gujrati
square
rectangle
parallelogram
trapezium
The correct Answer is:C
AP+PB+PC=PQ or AP+PB=PQ+CP
⇒AB=CQ
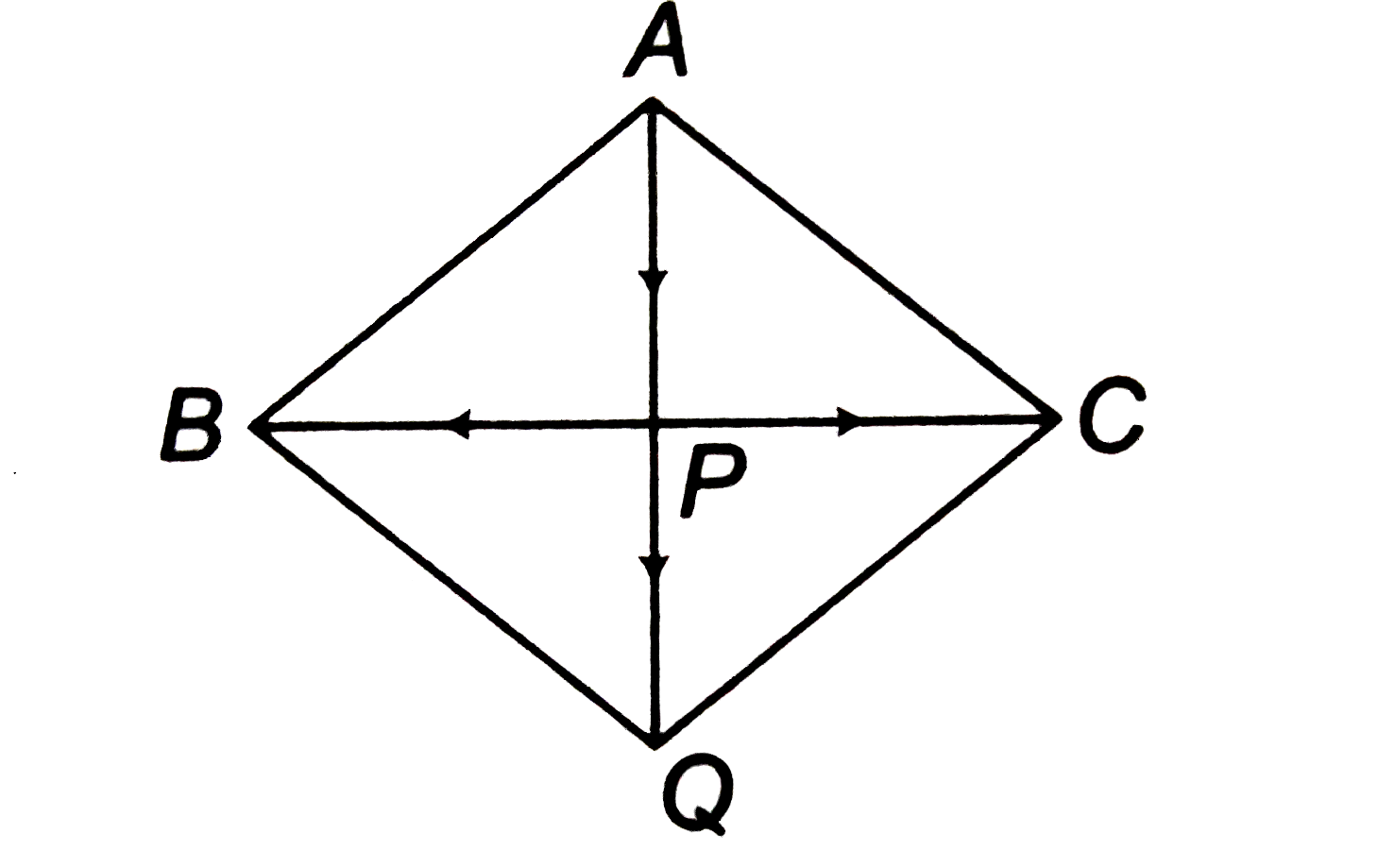
Hence, it is a parallelogram.
Similar Questions
P and Q are the points on sides AB and AC respectively of ΔABC. If AP = 3 cm, PB = 6 cm, AQ = 5 cm and QC = 10 cm, show that BC = 3 PQ.
View SolutionIn ΔABC, P and Q are points on sides AB and AC respectively. For each of the following cases, state whether PQ∣∣BC or not :
AP=8cm,PB=6cm,AQ=12cm,AC=21cm
View SolutionIn ΔABC, P and Q are points on sides AB and AC respectively. For each of the following cases, state whether PQ∣∣BC or not :
AP=8cm,PB=8cm,AQ=7cm,AC=15cm
View SolutionABC is any triangle and P is a point on the side BC. If Q is a point such that ¯¯¯¯¯¯PQ=¯¯¯¯¯¯AP+¯¯¯¯¯¯PB+¯¯¯¯¯¯PC, then
View SolutionDeltaABC P is a point in the interior of X, Y and Z. The points on the sides PA, PB and PC respectively are such that XY||AB And XZ||AC Prove that YZ||BC
View SolutionDeltaABC P is a point in the interior of X, Y and Z are the points PQ, PB and PC respectively in such a way that XY||AB And XZ||AC | Prove that YZ||BC .
View SolutionProve by vector method that in any triangle ABC, the point P being on the side −−→BC, if −−→PQ is the resultant of the vectors −−→AP, −−→PB and −−→PC, then ABQC is a parallelogram.
View SolutionIN any △ABC, a point p is on the side BC. If −−→PQis the resultant of the vectors −−→AP,−−→PB and −−→PC the prove that ABQC is a parallelogram and hence Q is a fixed point.
View Solution
