ABCD is a parallelogram. L is a point on BC which divides BC in the ratio 1:2. AL intersects BD at P.M is a point on DC which divides DC in the ratio 1:2 and AM intersects BD in Q.
Point P divides AL in the ratio Solution in Gujrati
1:2
1:3
3:1
2:1
The correct Answer is:C
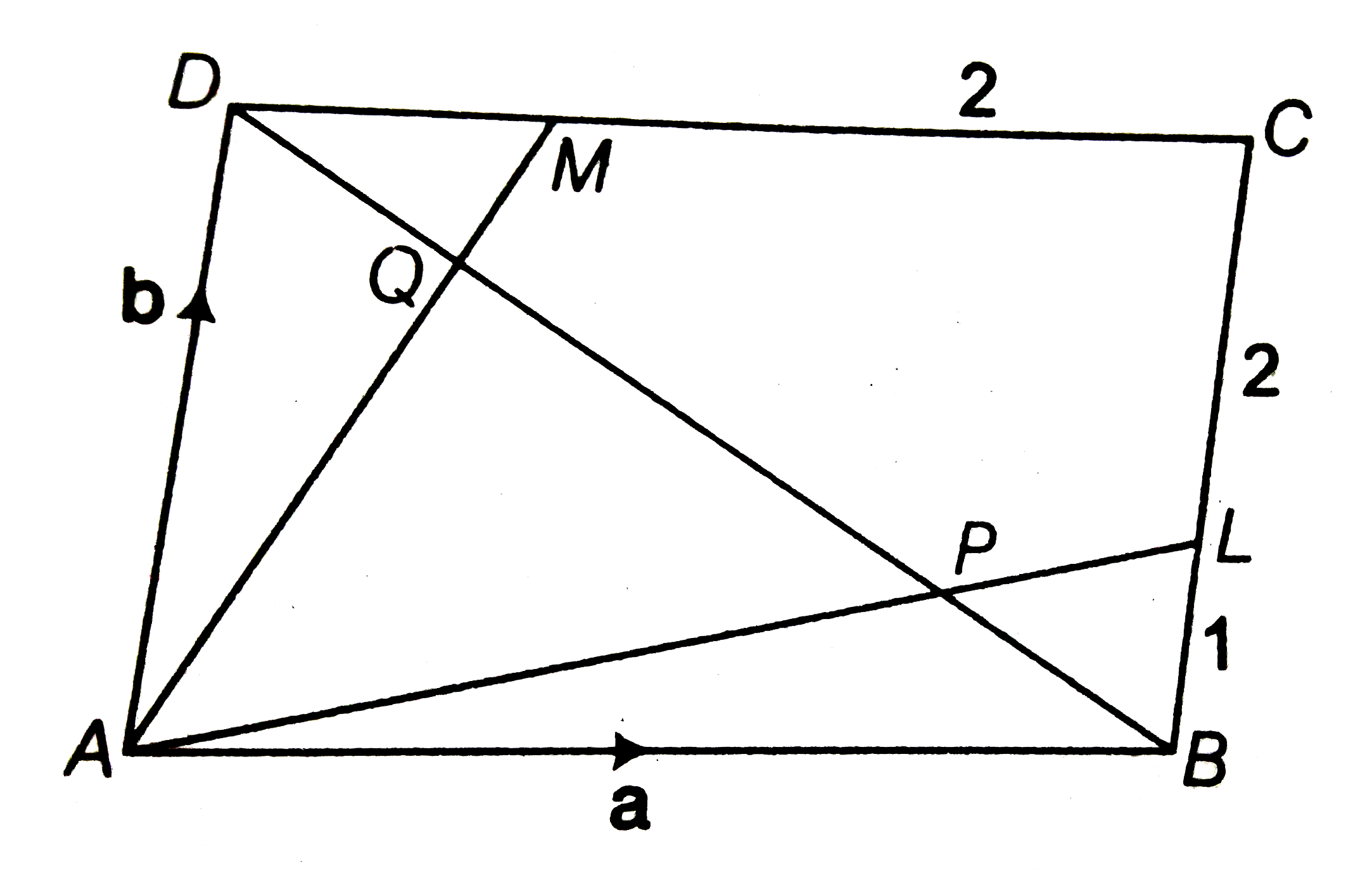
BL=13b
∴AL=a+13b
Let AP=λAL and P divides DB in the ratio μ:1−μ
Then, AP=λa+λ3b . . . (i)
Also, AP=μa+(1−μ)b . . (ii)
From eqs. (i) and (ii),
λa+λ3b=μa+(1−μ)b
∴λ=μ
and λ3=1−μ
∴λ=34
Similar Questions
ABCD is a parallelogram. L is a point on BC which divides BC in the ratio 1:2. AL intersects BD at P. M is a point on DC which divides DC in the ratio 1:2 and AM intersects BD in Q.
Point P divides AL in the ratio
View SolutionABCD is a parallelogram. L is a point on BC which divides BC in the ratio 1:2. AL intersects BD at P.M is a point on DC which divides DC in the ratio 1:2 and AM intersects BD in Q.
Point Q divides DB in the ratio
View SolutionABCD एक समांतर चतुर्भुज है, बिन्दु L, BC को अनुपात 1 : 2 में विभाजित करता है, AL, BD को बिन्दु P पर प्रतिच्छेद करता है बिन्दु M, DC को अनुपात 1 : 2 में तथा AM, BD को बिन्दु Q पर प्रतिछेद करता है |
बिन्दु P, AL को किस अनुपात में विभाजित करता है
View SolutionABCD एक समांतर चतुर्भुज है, बिन्दु L, BC को अनुपात 1 : 2 में विभाजित करता है, AL, BD को बिन्दु P पर प्रतिच्छेद करता है बिन्दु M, DC को अनुपात 1 : 2 में तथा AM, BD को बिन्दु Q पर प्रतिछेद करता है |
बिन्दु Q, DB किस अनुपात में विभाजित करता है
View SolutionABCD एक समांतर चतुर्भुज है, बिन्दु L, BC को अनुपात 1 : 2 में विभाजित करता है, AL, BD को बिन्दु P पर प्रतिच्छेद करता है बिन्दु M, DC को अनुपात 1 : 2 में तथा AM, BD को बिन्दु Q पर प्रतिछेद करता है |
PQ : DB बराबर है
View SolutionABCD is a parallelogram. L is a point on BC which divides BC in the ratio 1:2. AL intersects BD at P.M is a point on DC which divides DC in the ratio 1:2 and AM intersects BD in Q.
PQ:DB is equal to
View SolutionABCD is a parallelogram. L is a point on BC which divides BC in the ratio 1:2 . AL intersects BD at P.M is a point on DC which divides DC in the ratio 1 : 2 and AM intersects BD in Q. Point Q divides DB in the ratio
View Solution
