ABCD is a parallelogram. L is a point on BC which divides BC in the ratio 1:2. AL intersects BD at P.M is a point on DC which divides DC in the ratio 1:2 and AM intersects BD in Q.
PQ:DB is equal to
2/3
1/3
1/2
3/4
The correct Answer is:C
To solve the problem, we need to find the ratio PQ:DB in the given parallelogram ABCD with points L and M dividing segments BC and DC respectively.
1. Define the Vectors:
Let →A=→A (point A), →B=→A+→a (point B), →C=→B+→b=→A+→a+→b (point C), and →D=→A+→b (point D).
2. Find the Position of Point L:
Point L divides BC in the ratio 1:2. Using the section formula:
→L=2→B+1→C2+1=2(→A+→a)+1(→A+→a+→b)3=3→A+3→a+→b3=→A+→a+13→b
3. Find the Position of Point M:
Point M divides DC in the ratio 1:2:
→M=2→D+1→C2+1=2(→A+→b)+1(→A+→a+→b)3=3→A+2→b+→a3=→A+13→a+23→b
4. Find the Intersection Points P and Q:
The line AL can be represented parametrically as:
→R=→A+t(→L−→A)
The line BD can be represented as:
→R=→B+s(→D−→B)
Setting these equal to find P:
→A+t(→A+→a+13→b−→A)=→A+→a+s(→A+→b−(→A+→a))
Similarly, for point Q on line AM:
→R=→A+u(→M−→A)
5. Calculate the Ratios:
From the calculations above, we find that P divides DB in the ratio 3:1 and Q divides DB in the ratio 1:3.
6. Find the Lengths:
The length PQ can be expressed in terms of DB:
PQ = \frac{1}{2} DB \quad \text{(since PQ ishalfof DB )}
7. Final Ratio:
Therefore, the ratio PQ:DB is:
PQ:DB=12:1=1:2
Conclusion:
The final answer is:
PQ:DB=1:2
Let →A=→A (point A), →B=→A+→a (point B), →C=→B+→b=→A+→a+→b (point C), and →D=→A+→b (point D).
Point L divides BC in the ratio 1:2. Using the section formula:
→L=2→B+1→C2+1=2(→A+→a)+1(→A+→a+→b)3=3→A+3→a+→b3=→A+→a+13→b
Point M divides DC in the ratio 1:2:
→M=2→D+1→C2+1=2(→A+→b)+1(→A+→a+→b)3=3→A+2→b+→a3=→A+13→a+23→b
The line AL can be represented parametrically as:
→R=→A+t(→L−→A)
The line BD can be represented as:
→R=→B+s(→D−→B)
Setting these equal to find P:
→A+t(→A+→a+13→b−→A)=→A+→a+s(→A+→b−(→A+→a))
→R=→A+u(→M−→A)
From the calculations above, we find that P divides DB in the ratio 3:1 and Q divides DB in the ratio 1:3.
The length PQ can be expressed in terms of DB:
PQ = \frac{1}{2} DB \quad \text{(since PQ ishalfof DB )}
Therefore, the ratio PQ:DB is:
PQ:DB=12:1=1:2
The final answer is:
PQ:DB=1:2
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - INTRODUCTION TO VECTORS EXERCISE - MATRIX-MATCH TYPE3videos
INTRODUCTION TO VECTORS
- BOOK - CENGAGECHAPTER - INTRODUCTION TO VECTORS EXERCISE - Exercise (Numerical)6videos
INTRODUCTION TO VECTORS
- BOOK - CENGAGECHAPTER - INTRODUCTION TO VECTORS EXERCISE - LINKED COMPREHENSION TYPE2videos
INTRODUCTION TO VECTORS
- BOOK - CENGAGECHAPTER - INTEGRALSEXERCISE - Solved Examples And Exercises324videos
INTEGRALS
- BOOK - CENGAGECHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Question Bank24videos
INVERSE TRIGONOMETRIC FUNCTIONS
Similar Questions
Knowledge Check
- Question 1 - Select One
ABCD is a parallelogram. L is a point on BC which divides BC in the ratio 1:2. AL intersects BD at P.M is a point on DC which divides DC in the ratio 1:2 and AM intersects BD in Q.
Point Q divides DB in the ratioA1:2B1:3C3:1D2:1 - Question 2 - Select One
ABCD is a parallelogram. L is a point on BC which divides BC in the ratio 1:2. AL intersects BD at P.M is a point on DC which divides DC in the ratio 1:2 and AM intersects BD in Q.
Point P divides AL in the ratioA1:2B1:3C3:1D2:1 - Question 3 - Select One
In a quadrilateral ABCD, the point P divides DC in the ratio 1:2 and Q is the mid-point of AC. If AB+2AD+BC-2 DC=k PQ, then k is equal to
A−6B−4C6D4
ABCD is a parallelogram. E is a point on BC such that BE : EC = m:n. If AE and DB intersect in F, then what is the ratio of the area of triangle FEB to the area of triangle AFD?
View SolutionABCD is a parallelogram. L and M are points on AB and DC respectively and AL=CM. prove that LM and BD bisect each other.
View SolutionIn a quadrilateral ABCD, the point P divides DC in the ratio 1:2 and Q is the mid-point of AC. If AB+2AD+BC-2 DC=k PQ, then k is equal to
View SolutionIn a parallelogram ABCD, a side AB is extended to E such that BE = AB. If DE cut the line BC at Q then point Q divide BC in what ratio?
View SolutionABCD is a parallelogram and L is a point on DB . The produced line AL meets BC at M and DC produced at N .
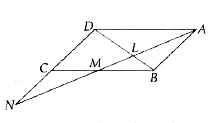
Given that DL =3LB , find ABCN .View Solution