In the Cartesian plane, a man starts at origin and walks a distance of 3 units of the north-east direction and reaches a point P. from P, he walks a distance of 4 units in the north-west direction to reach a point Q. construct the parallelogram OPQR with OP and PQ as adjacent sides. let M be the mid-point of PQ.
 Solution in Gujrati
Solution in Gujrati
The correct Answer is:A, B, C, D
(A) Let ˆiandˆj be the unit vectors along OX and OY respectively.
Now, OP=3 and a∩g≤XOP=45∘ implies that
OP=(3cos45∘)ˆi+(3sin45∘)ˆj=3√2(ˆi+ˆj)
(B) Again ∠XOR=135∘andOR=4 implies that
OR=4√2(−ˆi+ˆj)=2√2(−ˆi+ˆj)
(C) the position vector of Q is given by
OP+PQ=OP+OR=1√2(−ˆi+7ˆj)
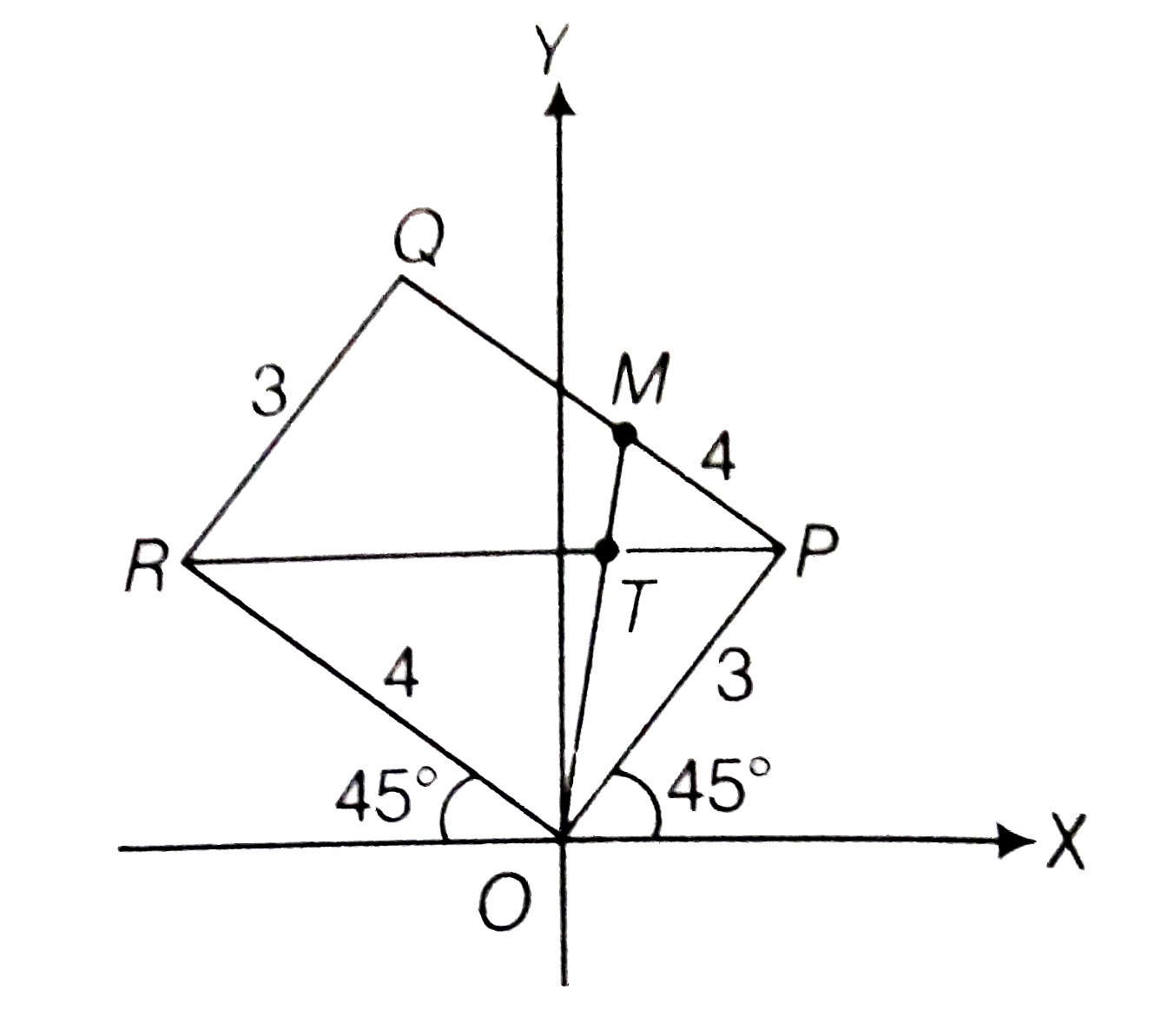
∴OM=(3√2)(ˆi+ˆj)+(1√2)(−ˆi+7ˆj)2
=2ˆi+10ˆj2√2=ˆi+5ˆj√2
(D) Now, PT:RT=1:2
thereofore, OT=1(OR)+2(OP)3
=(4√2)(−ˆi+ˆj)+2[(3√2)(ˆi+ˆj)]3
=√23(ˆi+5ˆj)
Similar Questions
कर्त्तीय समतल में, एक आदमी मूल बिन्दु से शुरू करके उत्तर पूर्व की दिशा में 3 इकाई की दूरी तय करके बिन्दु P पर पहुँचता है बिन्दु P से दक्षिण-पश्चिम की दिशा में 4 इकाई की दूरी तय करके बिन्दु Q पर पहुँचाता है इस प्रकार समांतर चतुर्भुज OPQR बनाया जाता है जिसकी दो आसन्न भुजाएँ PO तथा PQ है माना M, PQ का मध्य बिन्दु है

View SolutionIn the Cartesian plane, O is the origin of the coordinate axes. A person starts at 0 and walks a distance of 3 units in the NORTH - EAST direction and reaches the point P. From P he walks 4 units distance parallel to NORTH-WEST direction and reaches the point Q. then the vector OQ in terms i and j. (∠XOP=450) is
View SolutionIn the cartesian plane, O is the origin of the coordinate axes. A person starts at O and walks a distance of 3 units in the NORTH - EAST direction and reaches the point P. From P he walks 4 units distance parallel to NORTH - WEST direction and reaches the point Q. Express the vector ¯¯¯¯¯¯OQ interms of ¯iand¯j (Observe ∠XOP=45∘)
View SolutionA man walks a distance of 3 units from the origin towards the north east ( N45^@E) direction.from there he walks a distance of 4 units towards the north west (N45^@W) direction of reach a point P then the position of P in the Argand plane is :
View SolutionIn the cartesian plane, O is the origin of the coordinate axes. A person starts at O and walks a distance of 3 units in the NORTH - EAST direction and reaches the point P. From P he walks 4 units distance parallel to NORTH - WEST direction and reaches the point Q. Express the vector ¯¯¯¯¯¯OQ interms of ¯iand¯j (Observe ∠XOP=45∘)
View SolutionA man walks a distance of 3 units from the origin towards north-east to reach position A. from there he walks a distance of 4 units towards North west to reach position P. Then position of P in argand plane is
View SolutionAt point P, the value of (dy)/(dx) is : ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/ALN_PHY_R04_E01_025_Q01.png" width="80%"gt
View Solution
