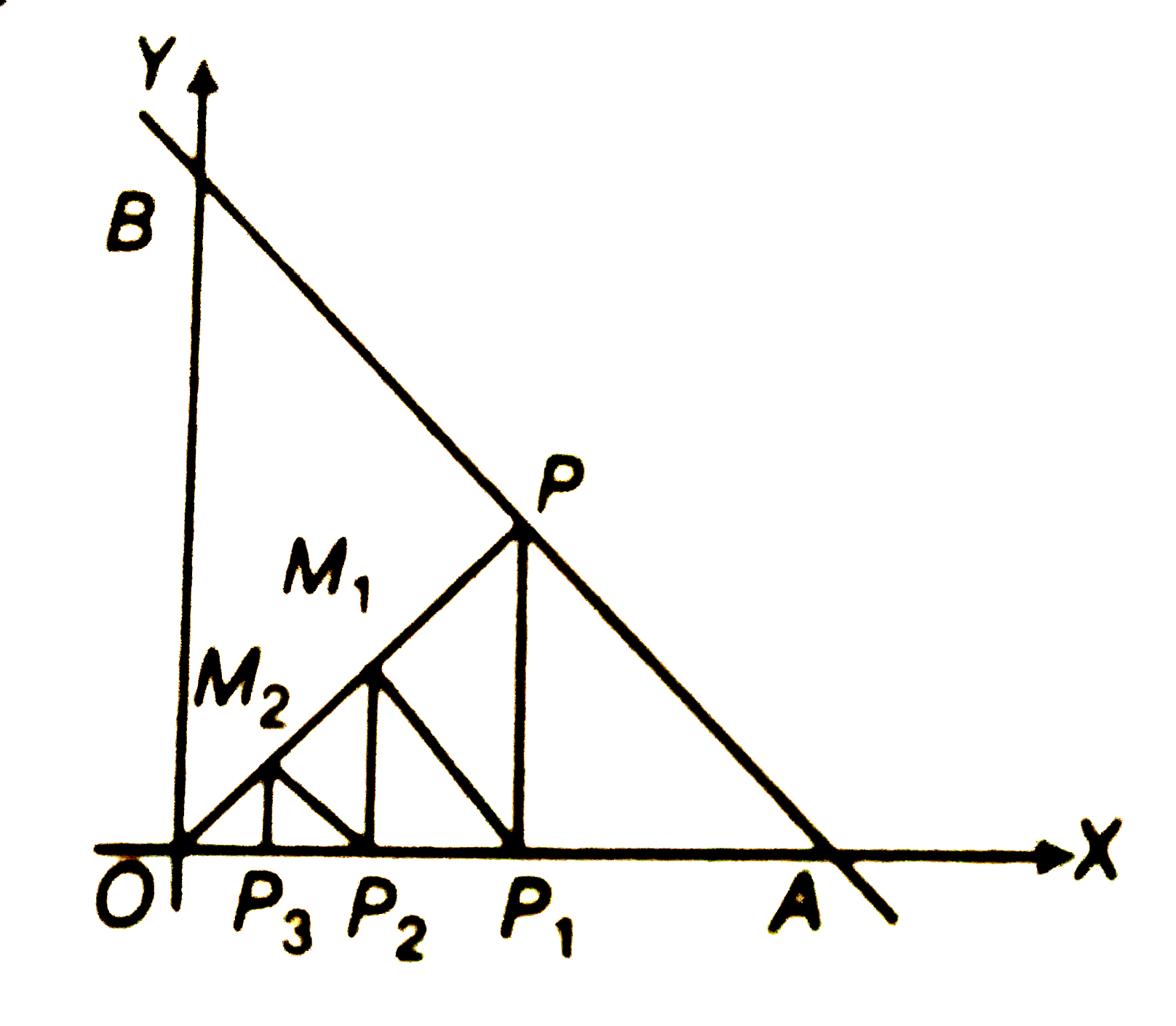
The line x+y=1 meets X-axis at A and Y-axis at B,P is the mid-point of AB,P1 is the foot of perpendicular from P to OA,M1 is that of P1 from OP,P2 is that of M1 from OA,M2 is that of P2 from OP,P3 is that of M2 from OA and so on. If Pn denotes theb nth foot of the perpendicular on OA, then find OPn
 .Solution in Gujrati
.Solution in Gujrati
We have, (OMn−1)2=(OPn)2+(PnMn−1)2
(OMn−1)2=(OPn)2+(OPn)2=2(OPn)2=2α2n[ say
Also, (OPn−1)2=(OMn−1)2+(Pn−1Mn−1)2
⇒α2n−1=α2n+12α2n−1⇒α2n=14α2n−1
⇒αn=12αn−1
⇒OPn=αn=122αn−2=...=12n
∴OPn=(12)n
Similar Questions
The line x+y=1 meets X-axis at A and Y-axis at B,P is the mid-point of AB,P1 is the foot ofperpendicular from P to OA,M1, is that of P1, from OP;P2, is that of M1 from OA,M2, is that of P2, from OP;P3 is that of M2, from OA and so on. If Pn denotes the nth foot of the perpendicular on OA, then find OPn.
View SolutionTwo bodies of different masses m1 and m2 have equal momenta. Their kinetic energies E1 and E2 are in the ratio
View SolutionThe line x+y=1 meets x-axis at A and y-axis at B,P is the midpoint of AB. P1 is the foot of the perpendicular from P to OA, M1 that form P1 to OP, P2 is that from M1 to OA and so on. If Pndenotes the nth foot of the perpendicualar on OA from Mn−1 then OPN
View Solutionरेखा x + y =1, x तथा y अक्षों को क्रमशः A तथा B बिन्दुओं पर मिलती हैं। बिन्दु P रेखा AB का मध्य-बिन्दु है, बिन्दु P से रेखा OA का लम्ब का पाद है। इसी प्रकार, P से रेखा OP का लम्ब का पाद M1 है, M1 से रेखा OA का लम्ब का पाद P2 है, P2 से रेखा OP का लम्ब का पाद M2 है और यदि Pn,Mn+1 से OP पर लम्ब के nवें मूल को प्रदर्शित करता है, तब OPn , का मान है
View SolutionIf p1,p2,p3 are respectively the perpendiculars from the vertices of ΔABC to the opposite sides, then
p1,p2,p3=
View SolutionThe line x+ y = 1 meets X-axis at A and Y-axis at B,P is the mid-point of AB, P_1 is the foot ofperpendicular from P to OA, M_1 , is that of P_1 , from OP;P_2 , is that of M_1 from OA, M_2 , is that of P_2 , from OP; P_3 is that of M_2 , from OA and so on. If P_n denotes the nth foot of the perpendicular on OA, then find OP_n .
View SolutionDetermice k so that the lines joining the points p1(k,1−,1) and P2(2k,0,2) shall be perpendicular to the line from P2 to P3(2+2k,k,1).
View Solution
