If an=34−(34)2+(34)3+...(−1)n−1(34)n and bn=1−an, then find the minimum natural number n, such that bn>an Solution in Gujrati
∴Bn=1−An>An⇒An<12
Now, An=34(1−(−34)n)1+34<12⇒(−34)n>−16
Obviously, it is true for all even values of n.
But for n=1,−34<−16
n=3(−34)3=−2724<−16
n=5,(−34)5=−2431024>−16
which is true for n=7 obviously, n0=7
Aliter Bn=1−An>An
⇒An<12⇒34(1−(−34)n)1+34<12⇒(−34)n>−16
Obviously, it is true for all even values of n.
But for n=1,−34<−16
n=3,(−34)3=−2764<−16
n=5,(−34)5=−2431024<−16
and for n=7⇒(−34)7=−218712288>−16
Hence, minimum natural number n0=7.
Similar Questions
Let An=(34)−(34)2+(34)3+….+(−1)n−1(34)nandBn=1−An.f∈dthe≤∗oddn∗uralνmebrsn_0, so that B_ngtA_n Aangen_0
View SolutionComplete the following statements.
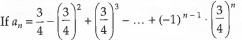 and bn=1−an then the smallest natural number n0, such that bn>anVntn>n0 is
and bn=1−an then the smallest natural number n0, such that bn>anVntn>n0 is
View SolutionThe Fibonacci sequence is defined by 1=a1=a2 and an=an−1+an−2, n>2. Find an+1an , for n = 1, 2, 3, 4, 5
View Solutionਫ਼ਿੱਬੋਨਾਕੀ ਅਨੁਕ੍ਰਮ ਹੇਠ ਲਿਖੇ ਅਨੁਸਾਰ ਪਰਿਭਾਸ਼ਿਤ ਹੈ 1=a1=a2 ਅਤੇ an=an−1+an−2, n>2 ਤਾਂ an+1an, n = 1, 2, 3, 4, 5 ਲਈ ਪਤਾ ਕਰੋ।
View SolutionLet An=(34)−(34)2+(34)3+.....+(−1)n−1(34)n , B_n = 1 - A_n . Find a least odd natural number n0, so that Bn>An∀n≥n0.
View SolutionLet f(x)=a_0+a_1x+a_2x^2++a_n x^n+ and (f(x))/(1-x)=b_0+b_1x+b_2x^2++b_n x^n+ , then b_n+b_(n-1)=a_n b. b_n-b_(n-1)=a_n c. b_n//b_(n-1)=a_n d. none of these
View SolutionIf an=34−(34)2+(34)3+...(−1)n−1(34)n and bn=1−an, then find the minimum natural number n, such that bn>an
View SolutionThe Fibonacci sequence is defined by 1=a1=a2andan=an−1+an−2,n>2. Find an+1an,for n = 1, 2, 3, 4, 5.
View Solution
