Two spherical soap bubble coalesce. If V is the consequent change in volume of the contained air and S the change in total surface area, show that
3PV+4ST=0
where T is the surface tension of soap bubble and P is
Atmospheric pressureSolution in Gujrati
The correct Answer is:n/a
Step by step video & image solution for Two spherical soap bubble coalesce. If V is the consequent change in volume of the contained air and S the change in total surface area, show that 3PV+4ST=0 where T is the surface tension of soap bubble and P is Atmospheric pressure by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLEN CHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 4 A (Fluid Statics)
13 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLEN CHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 4 A (Fuild Dynamics)
7 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLEN CHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 4 A (Elasticity)
7 Videos
- CENTRE OF MASSBOOK - ALLEN CHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-V B
19 Videos
- ERROR AND MEASUREMENTBOOK - ALLEN CHAPTER - ERROR AND MEASUREMENTEXERCISE - Part-2(Exercise-2)(B)
22 Videos
Similar Questions
A hydraulic automobile lift is designed to lift cars with a maximum mass of 3000Kg. The area of cross section of the piston carrying the load is 425cm2. What maximum pressures would the smaller piston have to bear?
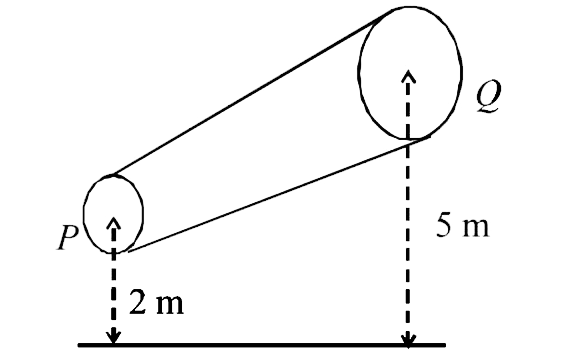
View SolutionA non-viscous liquid of constant density 1000kg/m3 flows in a streamline motion along a tube of variable cross section. The tube is kept inclined in the vertical plane as shown in Figure. The area of cross section of the tube two point P and Q at heights of 2 metres and 5 metres are respectively 4×10−3m2 and 8×10−3m2. The velocity of the liquid at point P is 1m/s. Find the work done per unit volume by the pressure and the gravity forces as the fluid flows from point P to Q.
View SolutionIn the figure shown the straing versus stress graph for two values of young's modulus ?
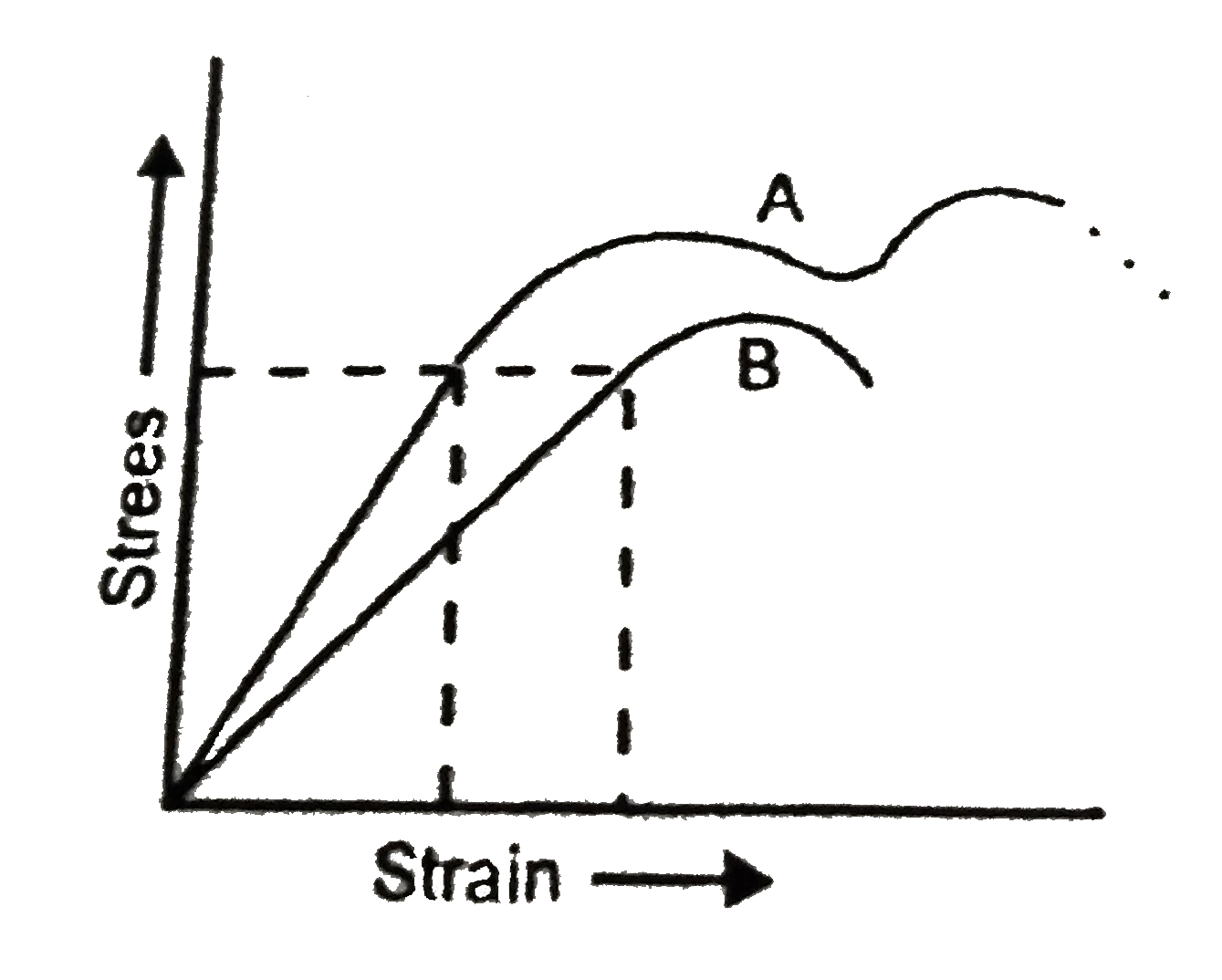
(i) which material is more ductile ? Explain.
(ii) Which material is more brittle ? Explain.
(iii) Which material is stronger ? Explain.
View SolutionTwo particles of masses m1 and m2 in projectile motion have velocities →v1 and →v2 , respectively , at time t=0. They collide at time t0. Their velocities become →v'1 and →v'2 at time 2t0 while still moving in air. The value of ∣∣∣(m1→v'1+m2→v'2)−(m1→v1+m2→v2)∣∣∣
View SolutionA cube has a side of length 1.2×10−2m. Calculate its volume.
View SolutionTwo spherical soap bubble coalesce. If V is the consequent change in volume of the contained air and S the change in total surface area, show that
3PV+4ST=0
where T is the surface tension of soap bubble and P is
Atmospheric pressure
View SolutionTwo soap bubbles of radii a and b coalesce to form a single bubble of radius c . If the external pressure is P , find the surface tension of the soap solution.
View SolutionTwo spherical soap bubble collapses. If V is the consequent change in volume of the contained air and S in the change in the total surface area and T is the surface tension of the soap solution, then it relation between P_(0), V, S and T are lambdaP_(0)V + 4ST = 0 , then find lambda ? (if P_(0) is atmospheric pressure) : Assume temperature of the air remain same in all the bubbles
View Solutionविभिन्न त्रिज्याओं वाले साबुन के घोल के दो बुलबुले मिलकर एक हो जाते है । यदि नये बुलबुले में भरी वायु के आयतन में परिवर्तन V हो तथा कुल पृष्ठ - क्षेत्रफल में परिवर्तन S हो , तो दर्शाइए कि 3PV+4ST=0, जहाँ T साबुन के घोल का पृष्ठ - तनाव है ।
View SolutionTwo spherical soap bubble coalese. If V be the change in volume of the contained air, A is the change in total surface area then show that 3PV+4AT=0 Where T is the surface tension and P is atmospheric pressure.
View SolutionTwo soap bubbles combine to form a single bubble. In this process, the change in volume and surface arca are respectively V and A. If p is the atmospheric pressure and T is the surface tension of the soap solution, the following relation is true.
View SolutionTwo spherical soap bubble coalesce. If ν be the change in volume of the contained air, A is the change in total surface area then show that 3PV + 4AT = 0 where T is the surface tension and P is atmospheric pressure.
View SolutionSurface Tension: Force due to Surface tension| Pressure difference across a spherical surface|Excess pressure in liquid drop| air bubble| soap bubble
View SolutionTwo soap bubble are combined isothermally to form a big bubble of radius R. If DeltaV is change in volume, DeltaS is change in surface area and P_(0) is atmospheric pressure then show that 3P_(0)(DeltaV)+4T(DeltaS)=0
View SolutionTwo soap bubbles combine under isothermal conditions to form a single soap bubble. If in this process, the change in volume is V and change in area is S, then ( P is atmospheric pressure)
View SolutionTwo spherical soap bubbles coalesce. If V is the consequent change in volume of the contained air S in the change in the total surface area. T is surface tension of the soap solution and P0 is the atmospheric pressure, then ST/P0V=-n/4, where n = --
View Solution
