When a vertical capillary of length l with a sealed upper end was brought in contact with the surface of a liquid, the level of this liquid rose to the height h. The liquid density is ρ, the inside diameter the capillary is d, the contact angle is θ, the atmospheric pressure is ρ0. Find the surface tension of the liquid. (Temperature in this process remains constant.)
 Solution in Gujrati
Solution in Gujrati
The correct Answer is:[ρgh+Pohl−h]d4cosθ
Step by step video & image solution for When a vertical capillary of length l with a sealed upper end was brought in contact with the surface of a liquid, the level of this liquid rose to the height h. The liquid density is rho, the inside diameter the capillary is d, the contact angle is theta, the atmospheric pressure is rho_(0). Find the surface tension of the liquid. (Temperature in this process remains constant.) by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLEN CHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 A (Previous year Questions)
29 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLEN CHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 B (MCQ)
13 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLEN CHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 4 A (Viscosity)
3 Videos
- CENTRE OF MASSBOOK - ALLEN CHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-V B
19 Videos
- ERROR AND MEASUREMENTBOOK - ALLEN CHAPTER - ERROR AND MEASUREMENTEXERCISE - Part-2(Exercise-2)(B)
22 Videos
Similar Questions
A wire suspended vertically from one of itsends is strached by attached a weight of 200N to the lower end . The weight streches the wire by 1mm . Then the elastic energy stored in the wire is
View SolutionWater from a tap emerges vertically downwards with an initial spped of 1.0ms−1. The cross-sectional area of the tap is 10−4m2. Assume that the pressure is constant throughout the stream of water, and that the flow is steady. The cross-sectional area of the stream 0.15 m below the tap is
View SolutionA flask contains glycerine and the other contains water. Both are stirred vigorously and placed on the table. In which flask will the liquid come to rest earlier and why?
View SolutionTwo particles of masses m1 and m2 in projectile motion have velocities →v1 and →v2 , respectively , at time t=0. They collide at time t0. Their velocities become →v'1 and →v'2 at time 2t0 while still moving in air. The value of ∣∣∣(m1→v'1+m2→v'2)−(m1→v1+m2→v2)∣∣∣
View SolutionA cube has a side of length 1.2×10−2m. Calculate its volume.
View Solution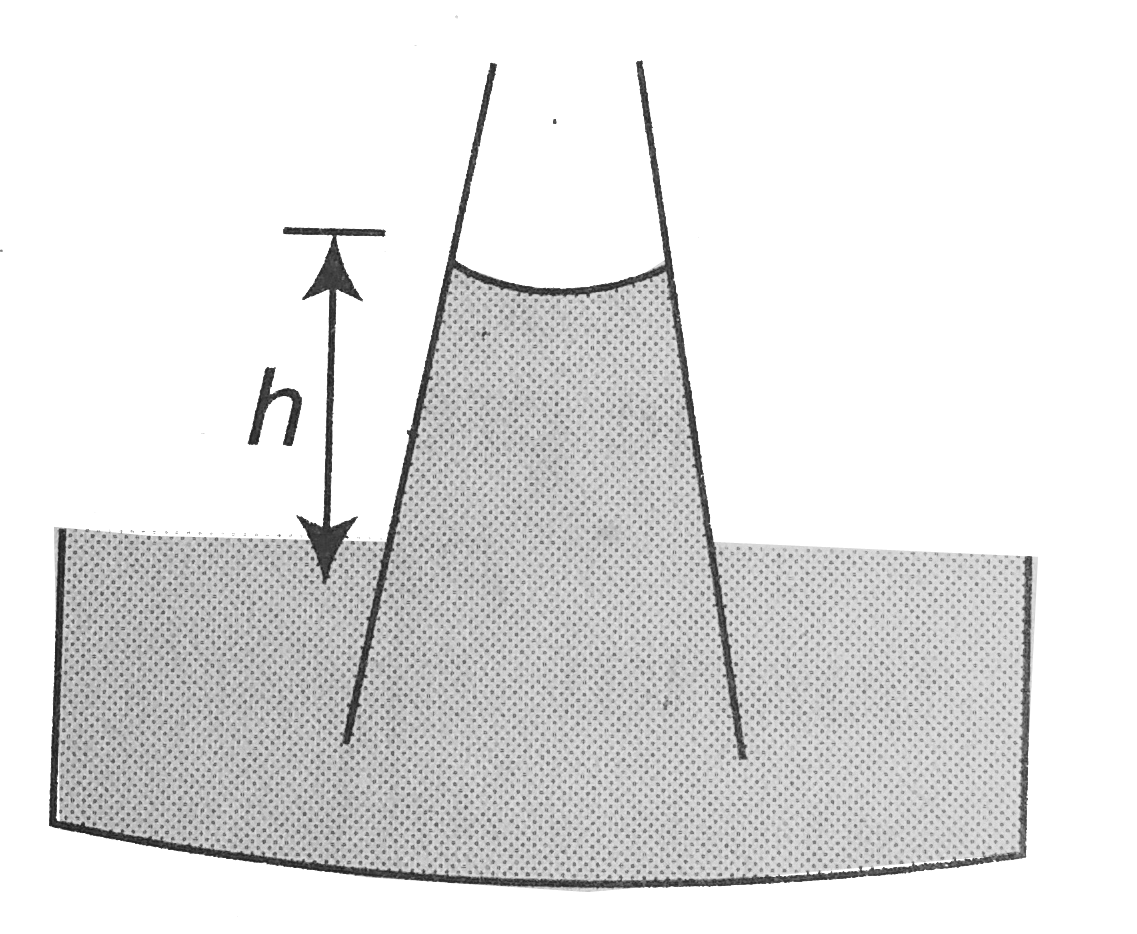
A capillary of the shape as shown is dipped in a liquid. Contact angle between the liquid and the capillary is 0∘ and effect of liquid inside the mexiscus is to be neglected. T is surface tension of the liquid, r is radius of the meniscus, g is acceleration due to gravity and ρ is density of the liquid then height h in equilibrium is:
View SolutionA capillary tube with inner cross-section in the form of a square of side a is dipped vertically in a liquid of density ρ and surface tension ρ which wet the surface of capillary tube with angle of contact θ . The approximate height to which liquid will be raised in the tube is : (Neglect the effect of surface tension at the corners of capillary tube)
View SolutionWhen one end of a tube of radius r is immersed vertically in a liquid of density rho , surface tension S, the rise of liquid in the tube is h and angle of contact is theta . If the tube is broken and its length is made h' (lt h) , then find the value of height of rise of liquid in the tube and angle of contact.
View SolutionA liquid of density rho and surface tension S rises to a height h in a capillary tube of diameter D. what is the weight of the liquid in the capillary tube? Angle of contact is 0^(@) .
View SolutionDuring capillary rise of a liquid in a capillary tube, the surface of contact that remains constant is of
View SolutionA capillary tube of radius r is lowered into a liquid of surface tension T and density rho . Given angle of contact =0^(@) . The work done by surface tension will be
View SolutionA long glass capillary (radius R) is taken out of liquid (surface tension S and density rho ) in vertical position. Angle of contact everywhere is zero. Atmospheric pressure is P_(0) . It is observed that the capillary retains some liquid. The length of liquid column retained in the capillary is
View SolutionThe height of liquid column in capillary tube is h the radius of capillary tube is r. rho is the density of liquid , g is acceleration due to gravity and theta is angle of contact . The surface tension of the liquid is ,
View SolutionWhen a capillary tube of radius r is dipped vertically in a liquid of surface tension T, the liquid rises to a height h in the tube above the level outside the tube . If the angle of contact is θ the density of the liquid is ρ then the pressure difference between the points A and B is

View SolutionA liquid of density rho and surface tension sigma rises in a capillary tube of diameter d. Angle of contact between the tube and liquid is zero. The weight of the liquid in the capillary tube is:
View SolutionA liquid of density ρ and surface tension σ rises in a capillary tube of diameter d. Angle of contact between the tube and liquid is zero.
In the above problem, the increase in gravitational potential energy of the liquid due to rise in the capillary is :
View Solution
