Calculate the mass of sun if the mean radius of the earth's orbit is 1.5×108km and G=6.67×10−11N×m2/kg2Solution in Gujrati
M=2×1030kg
M=3×1030
M=2×1015kg
M=3×1015kg
The correct Answer is:A
In case of orbital motion as v=√(GMr) so T=2πrv=2πr√rGM, i.e., M=4π2r3GT2
M=4×π2×(1.5×1011)36.67×10−11×(3.15×107)2 [as T=1 year =3.15×107s] i.e., M=2×1030kg
Topper's Solved these Questions
- GRAVITATIONBOOK - ALLEN CHAPTER - GRAVITATIONEXERCISE - Exercise 1 (Check your Grasp)
28 Videos
- GRAVITATIONBOOK - ALLEN CHAPTER - GRAVITATIONEXERCISE - Exercise 2 (Brain Teasers)
27 Videos
- GEOMETRICAL OPTICSBOOK - ALLEN CHAPTER - GEOMETRICAL OPTICSEXERCISE - subjective
14 Videos
- KINEMATICS-2DBOOK - ALLEN CHAPTER - KINEMATICS-2DEXERCISE - Exercise (O-2)
47 Videos
Similar Questions
Three identical point mass each of mass 1kg lie in the x-y plane at point (0,0), (0,0.2m) and (0.2m, 0). The net gravitational force on the mass at the origin is
View SolutionOne projectile after deviating from its path starts moving round the earth in a circular path of radius equal to nine times the radius of earth R. Its time period is
View SolutionA prism of refractive index n1 & another prism of reactive index n2 are stuck together without a gap as shown in the figure.The angle of the prisms are as shown. n1&n2depend onλ,the wavelength of light according to n1=1.20+10.8×104λ2&n2=1.45+1.80×104λ2 where λ is in nm.
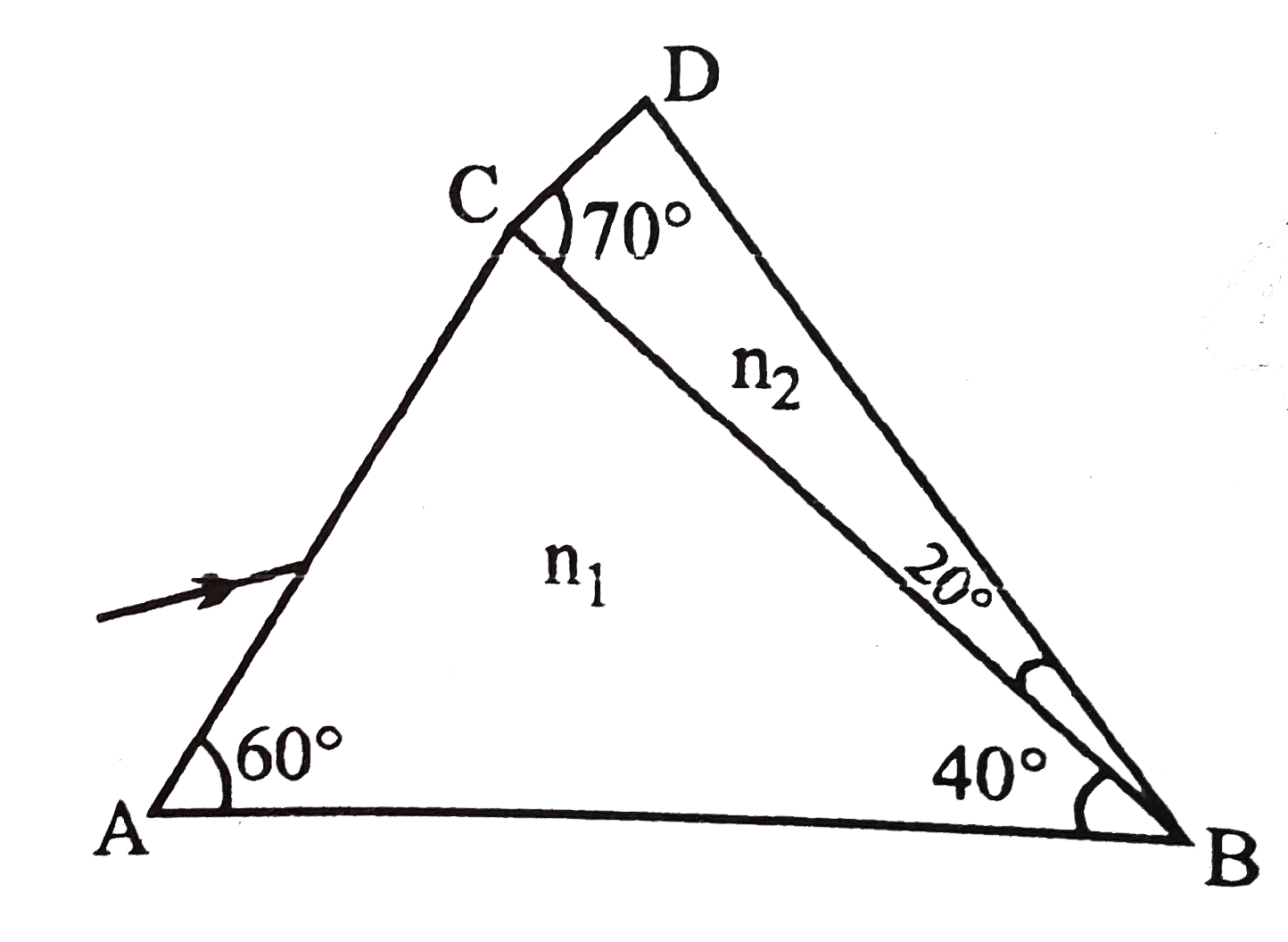
(i)Calculate the wavelength λ0for which rays incident at any angle on the interfaceBCpass through without bending at that interface.
(ii) for light of wavelength λ0,find the angle of incidencei on faceACsuch that the deviation produced by the combination of prism is minimum.
View SolutionA particle is moving in xy-plane .At certain instant the components of its velocity and acceleration are as follows ux=3m/s,uy=4m/s,ax=2m/s2anday=1m/s2. The rate of change of speed at this moment is
View SolutionCalculate mass of earth taking it to ne a sphere of radius 6400 km. given g=9.8 m//s^(2) and G=6.67xx10^(-11)N m^(2)kg^(-2)
View SolutionThe volume of mass and radius of sun are given by M_(o)=2xx10^(30)kg and R_(o)=7xx10^(5)km respectively. The pressure at the centre is bout (g=6.67xx10^(-11)m^(3).kg^(-1) s^(-2))
View SolutionThe mean radius of the earth's orbit round the sun is 1.5xx10^(11) . The mean radius of the orbit of mercury round the sun is 6xx10^(10)m . The mercury will rotate around the sun in
View SolutionFind the velocity of escape from the sun, if its mass is 1.89xx10^(30) kg and its distance from the earth is 1.59xx10^(8) km. Take G =6.67xx10^(-11) Nm^(2) kg^(-2)
View SolutionAssuming that earth's orbit around the sun is a circle of radius R=1.496xx10^(11)m compute the mass of the sun. (G=6.668xx10^(-11)Nm^(2)kg^(-2))
View Solutionएक उपग्रह पृथ्वी - तल से 2620 किमी की दूरी पर वृत्तीय कक्षा में घूम रहा है | उपग्रह के कक्षीय वेग तथा परिक्रमण - काल की गणना कीजिए | पृथ्वी की त्रिज्या = 6380 किमी, पृथ्वी का द्रव्यमान =6×1024 किग्रा तथा G=6.67×10−11 न्यूटन - मीटर 2/ किग्रा 2 |
View Solutionसूर्य के द्रव्यमान की गणना कीजिये यदि पृथ्वी की कक्षा की औसत त्रिज्या 1.5×108 किमी हो तथा G=6.67×10−11न्यूटन -मीटर2 किग्रा2 ।
View SolutionCalculate the force between the sun and jupiter. Assume that the mass of the sun =2×1030 kg, the mass of the jupiter = 1.89×1027 kg and the radius of the jupiter 's orbit =7.73×1011m .
(Use G=6.67×10−11Nm2/kg2 )
View SolutionFind the magnitude of the gravitational force between the Sun and the earth. (Mass of the Sun =2xx10^(30) kg, mass of the earth =6xx10^(24)kg and the distance between the centres of the Sun and the earth =1.5xx10^(11)m , (G=6.67xx10^(-11)N.m^(2)//kg^(2))
View SolutionThe mean radius of a planet is 6.67xx10^(3) km. The acceleration due to gravity on its surface is 10 m//s^(2) . If G = 6.67xx10^(-11)Nm^(2)//kg^(2) , then the mass of the planet will be [R=6.67xx10^(6)m]
View Solutionकिसी ग्रह की सूर्य के परितः परिक्रमण कक्षा की त्रिज्या 1.5×1011 मीटर एवं परिक्रमण काल 3.15×107 सेकण्ड हैं| सूर्य के द्रव्यमान की गणना कीजिए | G=6.67×10−11 N m2/Kg2 |
View SolutionThe mean orbital radius of the earth around the sun is 1.5xx10^(8) km. Calculate mass of the sun if G=6.67xx10^(-11)Nm^2"/"kg^(-2) ?
View Solution
