A prism of refractive index & another prism of reactive index are stuck together without a gap as shown in the figure.The angle of the prisms are as shown. depend on,the wavelength of light according to where is in nm.

(i)Calculate the wavelength for which rays incident at any angle on the interfacepass through without bending at that interface.
(ii) for light of wavelength ,find the angle of incidencei on facesuch that the deviation produced by the combination of prism is minimum.Solution in Gujrati
The correct Answer is:(a) 600 nm (b)
and
Here , is in nm.
(a) The incident ray will not deviate at BC if
= 1.45 + (1.80 xx 10^(4))/(lambda_(0)^(2)) (lambda = lambda_(0))implies (9 xx 10^(4))/(lambda_(0)^(2)) = 0.25 implies lambda_(0) = (3 xx 10^(2))/(0.5) "or" lambda_(0) = 600nm60^(@)r_(1) = r_(2) = (60^(@))/(2) = 30^(@)therefore n_(1) = ("sini")/("sinr")therefore "sini" = n_(1)"sin"30^(@)"sin i" = {1.20 + (10.8 xx 10^(4))/((600)^(2))}((1)/(2)) = (1.5)/(2) = (3)/(4)(lambda = lambda_(0) = 600 "nm")implies i = sin^(-1) (3//4)
_E01_244_S01.png)
Topper's Solved these Questions
Similar Questions
An optical component and an object S placed along its optic axis are given in Column I . The distance between the object and the component can be varied. The properties of images are given in Column II . Match all the properties of images from Column II with appropriate components given in Column I.
_E01_239_Q01.png)
View SolutionIn the Bohr's model of hy drogen atom, the electron moves around the nucleus in a circular orbit of radius 5×10−11m. Its time period is 1.5×10−16s. The current associated with the electron motion is:-
View SolutionAssertion : The difference in the value of acceleration due to gravity at pole and equator is proportional to square of angular velocity of earth.
Reason : the value of acceleration due to gravity is minimum at the equator and maximum at the pole.
View SolutionA overset(lambda)rarr B overset(2 lambda)rarr C T=0 ,N_(0) , 0 , T N_(1) N_(2) N_(3) The ratio of N_(1)" to "N_(2) is maximum I s
View SolutionA prism of refractive index n1 & another prism of reactive index n2 are stuck together without a gap as shown in the figure.The angle of the prisms are as shown. n1&n2depend onλ,the wavelength of light according to n1=1.20+10.8×104λ2&n2=1.45+1.80×104λ2 where λ is in nm.

(i)Calculate the wavelength λ0for which rays incident at any angle on the interfaceBCpass through without bending at that interface.
(ii) for light of wavelength λ0,find the angle of incidencei on faceACsuch that the deviation produced by the combination of prism is minimum.
View Solutionप्रकाश की एक किरण n1 अपवर्तनांक के एक माध्यम से n2 अपवर्तनांक के दूसरे माध्यम में जाती है। यदि आपतन कोण i है और अपवर्तन कोण r है, तो sinisinr किसके बराबर है?
View SolutionA light ray moving in medium-I (of refractive index n_(1) ) is incident on interface of two media and it is totally internally reflected at the interface. Now, refractive index n_(2) of medium-II is decreased, then
View Solutionएक प्रकाश किरण माध्यम (1) से माध्यम (2) में अपवर्तित होती है| इनके अपवर्तनांक क्रमश: n1 तथा n2 है तथा n2<n1 | क्रांतिक आपतन कोण के लिए व्यंजक लिखिए|
View Solutionअपवर्तनांक n1 का एक प्रिज्म तथा अपवर्तनांक n2 का एक दूसरा प्रिज्म परस्पर चित्रानुसार इस प्रकार दबाकर रखे गए हैं कि उनके बीच कोई अंतराल न रहे | प्रिज्मों के कोण चित्र में दर्शाए गए हैं | n1 तथा n2 तरंगदैर्ध्य पर निम्न प्रकार निर्भर करते हैं
n1=1.20+10.8×104λ2 तथा n2=1.45+1.80×104λ2
जहाँ λ नैनोमीटर में है |
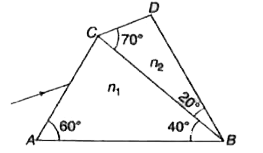
(a) उन प्रकाश किरणों की तरंगदैर्ध्य λ0 की गणना कीजिए जोकि अंतरापृष्ठ BC पर किसी भी कोण पर आपतित होने पर अंतरापृष्ठ में से बिना मुड़े गुजर जाए | (b) तरंगदैर्ध्य λ0 की प्रकाश किरणों के लिए, पृष्ठ AC पर वह आपतन कोण ज्ञात कीजिए, जिसके लिए प्रिज्मों के संयोग से उत्पन्न विचलन न्यूनतम हो |
View Solution(a) In Fig. 32-19a, a beam of monochromatic light reflects and refracts at point A on the interface between material 1 with index of refraction n1 = 1.33 and material 2 with index of refraction n2=1.77. The incident beam makes an angle of 50∘) with the interface. What is the angle of reflection at poinl A ? What is the angle of refraction there?
View SolutionA ring angled isosceles prism KLM of refractive index n_(1) is placed inside a rectangular block PQRS of refractive index n_(2) as shown in the adjoining Fig. The rectangular box is surrounded by a medium of refractive index n_(3) . A ray of light AB enters the rectangular block normally. Depending upon the relationships between n_(1), n_(2) and n_(3) . it takes one of the four possible paths. Under what condition the ray follows the path no. 1 (i.e., path ABCI)?
View SolutionA ring angled isosceles prism KLM of refractive index n1 is placed inside a rectangular block PQRS of refractive index n2 as shown in the adjoining Fig. The rectangular box is surrounded by a medium of refractive index n3. A ray of light AB enters the rectangular block normally. Depending upon the relationships between n1,n2andn3. it takes one of the four possible paths.
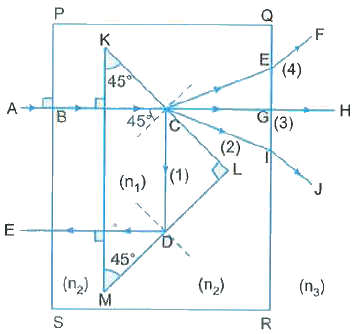
Under what condition the ray follows the path no. 2 (i.e., path ABCIJ)?
View SolutionA ring angled isosceles prism KLM of refractive index n_(1) is placed inside a rectangular block PQRS of refractive index n_(2) as shown in the adjoining Fig. The rectangular box is surrounded by a medium of refractive index n_(3) . A ray of light AB enters the rectangular block normally. Depending upon the relationships between n_(1), n_(2) and n_(3) . it takes one of the four possible paths. State the condition for light ray to travel along path no. 3 (i.e., path ABCGH).
View SolutionA ring angled isosceles prism KLM of refractive index n_(1) is placed inside a rectangular block PQRS of refractive index n_(2) as shown in the adjoining Fig. The rectangular box is surrounded by a medium of refractive index n_(3) . A ray of light AB enters the rectangular block normally. Depending upon the relationships between n_(1), n_(2) and n_(3) . it takes one of the four possible paths. What is the condition for light ray to proceed along the path no. 4 (i.e., path ABCEF)?
View Solutionn_(1) A prism of refractive index and n_(2) The second prism of the refractive index is located by sticking to each other without cracks as shown in the figure. Prism angles are shown. n_(1) and n_(1),n_(1)=1.20+(10.8xx10^(-4))/( lambda^(2)) and n_(2)=1.45+(1.80xx10^(4))/(lambda^(2)) According to the wavelength of light lambda Depends on where lambda, nm Is in (i) For rays incident at any angle on the interleaved BC, which pass through the same surface without turning, the wavelength of lambda Calculate (ii) lambda_(0) For wavelength light, find the incidence angle of i on pane AC so that the deviation produced by the combination of prismo is minimal.
View SolutionA overset(lambda)rarr B overset(2 lambda)rarr C T=0 N_(0) , 0 , 0 T= N_(1) N_(2) N_(3) The ratio of N_(1)" to "N_(2) is maximum I s
View Solution
