Two wave are represented by the equations y1=asinωt ad y2=acosωt the first waveSolution in Gujrati
leads the second by π
lags the seconds by π
leads the seconds by π2
lags the seconds by π2
The correct Answer is:D
y1=asinωt=acos(ω−π/2)
y2=acosωt
Topper's Solved these Questions
- WAVE OPTICSBOOK - ALLEN CHAPTER - WAVE OPTICSEXERCISE - Exercise 2 (Brain Teasures)
22 Videos
- WAVE OPTICSBOOK - ALLEN CHAPTER - WAVE OPTICSEXERCISE - Exercise 3 (Miscellaneous type Questions)
27 Videos
- WAVE OPTICSBOOK - ALLEN CHAPTER - WAVE OPTICSEXERCISE - Example 15
1 Videos
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR BOOK - ALLEN CHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (J-A)
7 Videos
Similar Questions
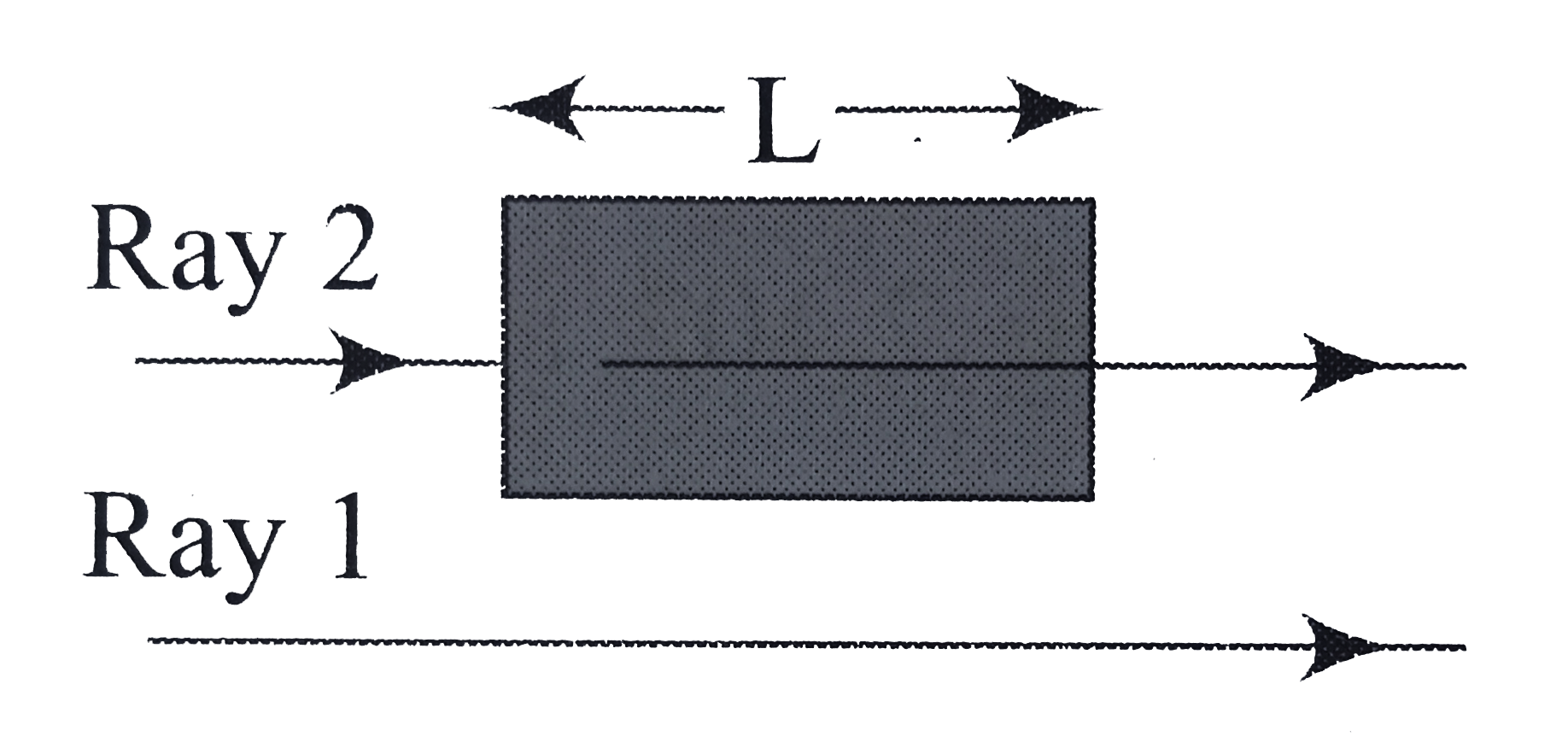
As shown in figure waves with identical wavelengths and amplitudes and which are intially in phase travel through difference media. Ray 1 travels through air and Ray 2 through a transparent medium for equal length L, in four different situations. Rays reach a common point on the screen. The number of wavelengths in length L is N2 for Ray 2 and N1 for Ray 1. In the following table, values of N1 and N2 are given for all four situations. The order or the situations according to the intensity of the light at the common point in descending order is Situations
1 2 3 4
N1 2.75 1.80 3.00 3.25
N2 2.75 2.80 3.25 4.00
View SolutionStatement-1: if white light is used in YDSE, then the central bright fringe will be white.
Statement-2: In case of white light used in YDSE all the wavelengths produce their zero order maxima at the same position.
View Solution_S01_033_Q01.png)
In a typical young's double slit experiment a point source of monochromatic light is kept as shown in the figure. If the source is given an instantaneous velocity v=1 mm per second towards the screen, then the instantaneous velocity of central maxima is given as α×10−βcm/s upward in scientific notation find the value of α+β
View SolutionMatch List I with List II and select the correct answer using the codes given below the lists :

View SolutionTwo light waves are represented by y_(1)=a sin_(omega)t and y_(2)= a sin(omega t+delta) . The phase of the resultant wave is
View SolutionIf two waves represented by y1=4sinωt and y2=3sin(ωt+π3) interfere at a point find out the amplitude of the resulting wave
View SolutionThe resultant amplitude of a vibrating particle by the superposition of the two waves y_(1)=asin[omegat+(pi)/(3)] and y_(2)=asinomegat is
View SolutionTwo wave are represented by equation y_(1) = a sin omega t and y_(2) = a cos omega t the first wave :-
View SolutionTwo waves are represented by: y1=4sin404πt and y2=3sin400πt. Then :
View Solutionदो तरंगों के विस्थापन समीकरण y1=asinωt तथा y2=acosωt हैं । दूसरी तरंग के सापेक्ष पहली तरंग की कला कितनी होगी -
View Solutiony_(1)=Asin(omegat-kx)&y_(2)=Asin(omegat-kx+delta) : these two equations are representing two waves. Then the amplitude of the resulting wave is
View Solutionदो तरंगों के समीकरण है
y1=asin(ωt−kx) तथा y2=acos(ωt–kx)
दो तरंगों के बीच कलांतर है
View SolutionTwo waves given by y_(1)=asinomegat and y_(2)=a sin (omegat+pi//2) reaching at a point superimpose. The resultant amplitude is
View SolutionThe two waves are displayed as follows y_(1)=a sin omega t y_(2)=a cos omega t The first wave is from the second …………………
View SolutionIf two waves represented by y_(1)=4sinomegat and y_(2)=3sin(omegat+(pi)/(3)) interfere at a point find out the amplitude of the resulting wave
View Solutionदो तरंगों का विस्थापन निम्न से दर्शाया जाता है, y1=Asin200πt और y2=Asin208πt. एक तरंग का सामान्य समीकरण y=Asin2πvt से दिया जाता है। उपर्युक्त दोनों तरंगों को एक साथ ध्वनित किया जाता है, तब हम पायेंगे-
View Solution
