The lens governing the behavior of the rays namely rectilinear propagation laws of reflection and refraction can be summarised in one fundamental law known as Fermat's principle. According to this principle a ray of light travels from one point to another such that the time taken is at a stationary value (maximum or minimum).
if c is the velocity of light in a vacuum the velocity in a medium of refractive index μ is cμ hence time taken to travel a distance l is μlc if the light passes through a number of media, the total time taken is (1c)∑μl or 1c∫μdl if refractive index varies continuously. Now ∑μl is the total path, so that fermat's principle states that the path of a ray is such that the optical path in at a stationary value. this principle is obviously in agreement with the fact that the ray are straight lines i a homogenous isotropic medium. it is found that it also agrees with the classical laws of reflection and refraction.
Q. If refractive index of a slab varies as μ=1+x2 where x is measured from one end then optical path length of a slab of thickness 1 m isSolution in Gujrati
43m
34m
1m
none
The correct Answer is:A
Optical path length
=∫μdx=∫10(1+x2)dx=(x+x33)10=43m
Topper's Solved these Questions
- WAVE OPTICSBOOK - ALLEN CHAPTER - WAVE OPTICSEXERCISE - Exercise 4 A (Conceptual subjective Exercise)
9 Videos
- WAVE OPTICSBOOK - ALLEN CHAPTER - WAVE OPTICSEXERCISE - Exercise 4 B (Conceptual subjective Exercise)
8 Videos
- WAVE OPTICSBOOK - ALLEN CHAPTER - WAVE OPTICSEXERCISE - Exercise 2 (Brain Teasures)
22 Videos
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR BOOK - ALLEN CHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (J-A)
7 Videos
Similar Questions
Consider interference between two sources of intensity I and 4I. Find out resultant intensity where phase difference is (i). π/4
(ii). π
(iii). 4π
View SolutionTwo identical monochromaticlight sources A & B intensity 10−15W/m2 produce wavelength of light 4000√3Å A glass of thickness 3mm is placed in the path of the ray as shown in figure the glass has a varible refractive index n=1+√x where x (in mm) is distance of plate from left to right calculate total intensity at focal points F of the lens.
_E01_100_Q01.png)
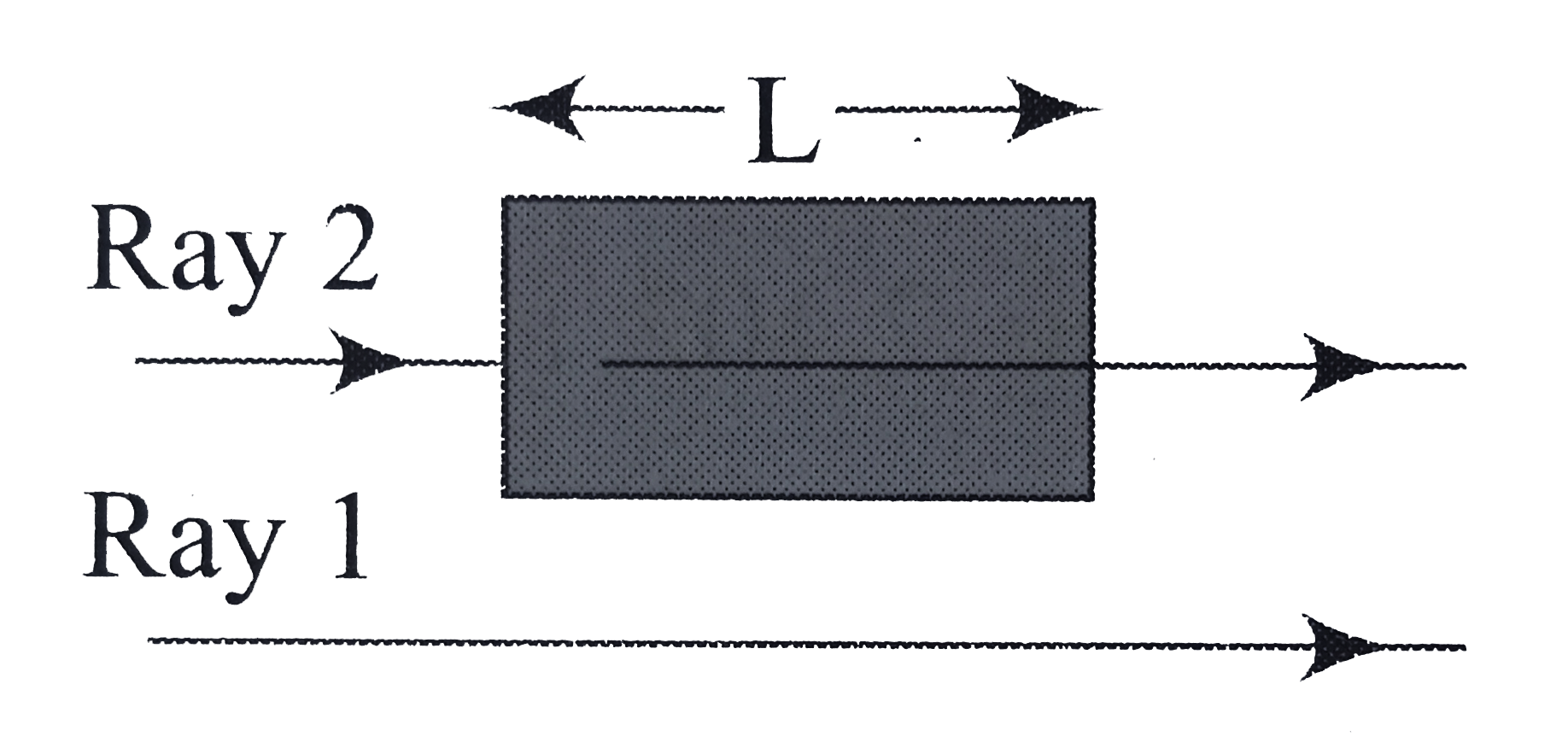
View SolutionAs shown in figure waves with identical wavelengths and amplitudes and which are intially in phase travel through difference media. Ray 1 travels through air and Ray 2 through a transparent medium for equal length L, in four different situations. Rays reach a common point on the screen. The number of wavelengths in length L is N2 for Ray 2 and N1 for Ray 1. In the following table, values of N1 and N2 are given for all four situations. The order or the situations according to the intensity of the light at the common point in descending order is Situations
1 2 3 4
N1 2.75 1.80 3.00 3.25
N2 2.75 2.80 3.25 4.00
View SolutionMatch List I with List II and select the correct answer using the codes given below the lists :

View SolutionThe lens governing the behavior of the rays namely rectilinear propagation laws of reflection and refraction can be summarised in one fundamental law known as Fermat's principle. According to this principle a ray of light travels from one point to another such that the time taken is at a stationary value (maximum or minimum). if c is the velocity of light in a vacuum the velocity in a medium of refractive index mu is (c)/(mu) hence time taken to travel a distance l is (mul)/(c) if the light passes through a number of media, the total time taken is ((1)/(c))summul or (1)/(c)intmudl if refractive index varies continuously. Now summul is the total path, so that fermat's principle states that the path of a ray is such that the optical path in at a stationary value. this principle is obviously in agreement with the fact that the ray are straight lines i a homogenous isotropic medium. it is found that it also agrees with the classical laws of reflection and refraction. Q. The optical path length followed by ray from point A to B given that laws of refraction are obeyed as shown in figure.
View SolutionThe lens governing the behavior of the rays namely rectilinear propagation laws of reflection and refraction can be summarised in one fundamental law known as Fermat's principle. According to this principle a ray of light travels from one point to another such that the time taken is at a stationary value (maximum or minimum). if c is the velocity of light in a vacuum the velocity in a medium of refractive index mu is (c)/(mu) hence time taken to travel a distance l is (mul)/(c) if the light passes through a number of media, the total time taken is ((1)/(c))summul or (1)/(c)intmudl if refractive index varies continuously. Now summul is the total path, so that fermat's principle states that the path of a ray is such that the optical path in at a stationary value. this principle is obviously in agreement with the fact that the ray are straight lines i a homogenous isotropic medium. it is found that it also agrees with the classical laws of reflection and refraction. Q. The optical length followed by ray from point A to B given that laws of reflection are obeyed as shown in figure is
View SolutionA ray of light travelling with a speed c leaves point 1 shown in figure and is reflected to point 2. The ray strikes the reflecting surface at a distance x from point 1. According to Fermat's principle of least time, among all possible paths between two points , the one actually taken by a ray of light is that for which the time taken is the least (In fact there are some cases in which the time taken by a ray is maximum rather than a minimum).
_S01_058_Q01.png)
Find the time for the ray to reach from point 1 to point 2.
View SolutionA ray of light travelling with a speed c leaves point 1 shown in figure and is reflected to point 2. The ray strikes the reflecting surface at a distance x from point 1. According to Fermat's principle of least time, among all possible paths between two points , the one actually taken by a ray of light is that for which the time taken is the least (In fact there are some cases in which the time taken by a ray is maximum rather than a minimum).
_S01_059_Q01.png)
Under what condition is time taken least?
View SolutionA ray of light travelling with a speed c leaves point 1 shown in figure and is reflected to point 2. The ray strikes the reflecting surface at a distance x from point 1. According to Fermat's principle of least time, among all possible paths between two points , the one actually taken by a ray of light is that for which the time taken is the least (In fact there are some cases in which the time taken by a ray is maximum rather than a minimum).
_S01_060_Q01.png)
Which of the following statement is in accordance with Fermat's principle
View SolutionA light ray is travelling from air to medium, c is velocity of light in air and v is velocity of light in medium. The reflected and refracted rays are perpendicular to each other. The angle of polarisation is
View SolutionThe change in the __________ of light rays while going from one medium to another is called refraction.
View SolutionRefraction of light is the phenomenon of change in the path of light ray when it goes from one medium to another. State the laws of refraction
View SolutionRay of light bends as light travels from one medium to another.
View SolutionThe phase velocity of light in a plasma exceeds the velocity of light in a vacuum. Is this not in contradiction with the fundamental principle of the theory of relativity that the fundamental principle of the theory of relativity that the velocity of light in a vacuum is the maximum pos- sible velocity?
View SolutionThe lens governing the behavior of the rays namely rectilinear propagation laws of reflection and refraction can be summarised in one fundamental law known as Fermat's principle. According to this principle a ray of light travels from one point to another such that the time taken is at a stationary value (maximum or minimum). if c is the velocity of light in a vacuum the velocity in a medium of refractive index mu is (c)/(mu) hence time taken to travel a distance l is (mul)/(c) if the light passes through a number of media, the total time taken is ((1)/(c))summul or (1)/(c)intmudl if refractive index varies continuously. Now summul is the total path, so that fermat's principle states that the path of a ray is such that the optical path in at a stationary value. this principle is obviously in agreement with the fact that the ray are straight lines i a homogenous isotropic medium. it is found that it also agrees with the classical laws of reflection and refraction. Q. The optical path length followed by ray from point A to B given that laws of refraction are obeyed as shown in figure.
View SolutionThe lens governing the behavior of the rays namely rectilinear propagation laws of reflection and refraction can be summarised in one fundamental law known as Fermat's principle. According to this principle a ray of light travels from one point to another such that the time taken is at a stationary value (maximum or minimum). if c is the velocity of light in a vacuum the velocity in a medium of refractive index mu is (c)/(mu) hence time taken to travel a distance l is (mul)/(c) if the light passes through a number of media, the total time taken is ((1)/(c))summul or (1)/(c)intmudl if refractive index varies continuously. Now summul is the total path, so that fermat's principle states that the path of a ray is such that the optical path in at a stationary value. this principle is obviously in agreement with the fact that the ray are straight lines i a homogenous isotropic medium. it is found that it also agrees with the classical laws of reflection and refraction. Q. The optical length followed by ray from point A to B given that laws of reflection are obeyed as shown in figure is
View Solution
