Statement-1: Two longitudinal waves given by equation y1(x,t)=2asin(ωt−kx)
and y2(x,t)=asin(2ωt−2kx)
will have equal intensity.
Statement-2 : Intensity of waves of given frequency in same medium is proportional to square of amplitude only. Solution in Gujrati
Statement-1 is flase, statement-2 is true
Statement-1 is true, Statement-2 is false
Statement-1 is true, Statement-2 true , Statement-2 is the correct axplanation of statement-1
Statement-1 is true, Statement-2 is true , Statement-2 is not correct explanation of Statement-1.
The correct Answer is:B
y1(x,t)=2asin(wt−kx)
y2(x,t)=asin(2wt−2kx)
I=2π2n2a2ρv⇒I1I2=(2aa×n2n)2=11
Intensity depends on frequency and amplitude
So statememt-1 is true statement-2 is false.
Topper's Solved these Questions
- WAVES AND OSCILLATIONSBOOK - ALLEN CHAPTER - WAVES AND OSCILLATIONSEXERCISE - Part-1(Exercise-05)[B]
42 Videos
- WAVES AND OSCILLATIONSBOOK - ALLEN CHAPTER - WAVES AND OSCILLATIONSEXERCISE - Part-1(Exercise-04)[B]
13 Videos
- SEMICONDUCTORSBOOK - ALLEN CHAPTER - SEMICONDUCTORSEXERCISE - Part-3(Exercise-4)
50 Videos
Similar Questions
A string of length 0.4m and mass 10−2kg is clamped at one end . The tension in the string is 1.6N. The identical wave pulses are generated at the free end after regular interval of time , Δt . The minimum value of Δt , so that a constructive interference takes place between successive pulses is
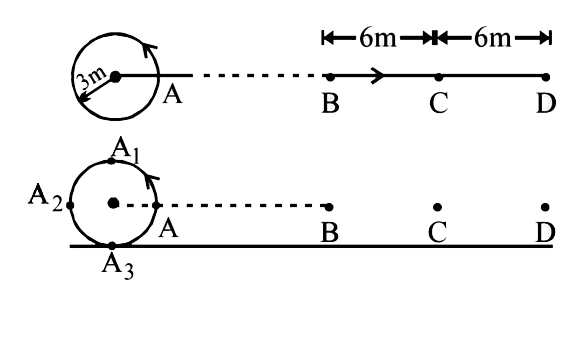
View SolutionA source of sound is moving along a circular orbit of radius 3meter with an angular velocity of 10rad/s. A sound detector located far away from the source is executing linear simple harmonic motion along the line BD with an amplitude BC=CD=6meters. The frequency of oscillation of the detector is 5π per second. The source is at the point A when the detector is at the point B. If the source emits a continuous sound wave of frequency 340Hz, Find the maximum and the minimum frequencies recorded by the detector.
View SolutionAt absolute zero temperature Si acts as ……..
View SolutionStatement-1: Two longitudinal waves given by equation y1(x,t)=2asin(ωt−kx)
and y2(x,t)=asin(2ωt−2kx)
will have equal intensity.
Statement-2 : Intensity of waves of given frequency ini same medium is proportioal to square of amplitude only.
View SolutionTwo waves are given by y1=asin(ωt−kx) and y2=acos(ωt−kx). The phase difference between the two waves is -
View Solutionकथन 1 : अनुदैर्घ्य तरंगों y1=2asin(ωt−kx)तथा2=asin(2ωt−2kx) की तीव्रताएँ समान होंगी। कथन 2 : किसी माध्यम में नियत आवृत्ति से गमन करने वाली तरंगों की तीव्रता, आयाम के वर्ग के अनुक्रमानपाती होती है।
View SolutionTwo waves y_(1) = a sin (omegat - kx) and y_(2) = a cos(omegat - kx) superimpose at a point :
View Solutiony_(1)=Asin(omegat-kx)&y_(2)=Asin(omegat-kx+delta) : these two equations are representing two waves. Then the amplitude of the resulting wave is
View Solutionবিবৃতি 1. দুটি অনুদৈর্ঘ্য তরঙ্গের সমীকরণ যথাক্রমে y1=2asin(ωt–kx) এবং y2=asin(2ωt−2kx)। এদের তীব্রতা সমান। বিবৃতি 2. একটি নির্দিষ্ট মাধ্যমে নির্দিষ্ট কম্পাঙ্কের তরঙ্গের তীব্রতা তার বিস্তারের বর্গের সমানুপাতিক।
View SolutionStatement - 1 : Two longitudinal waves given by equations : y_(1) (x,t) = 2 a sin (omega t- kx) and y_(2) (x,t) = a sin (2 omega t - 2kx) will have equal intensity . Statement -2 : Intensity of waves of given frequency in same medium is proportional to square of amplitude only .
View Solutionकथन 1 : अनुदैर्घ्य तरंगों y1=2asin(ωt−kx)तथा2=asin(2ωt−2kx) की तीव्रताएँ समान होंगी। कथन 2 : किसी माध्यम में नियत आवृत्ति से गमन करने वाली तरंगों की तीव्रता, आयाम के वर्ग के अनुक्रमानपाती होती है।
View Solutionसमान दिशा में गतिमान तरंगो का y1=Asin(ωt−kx),y2=Asin(ωt−kx−θ) है माध्यम के कणो का आयाम होगा
View SolutionY1=asinωt तथा Y2=asin(ωt+δ) वाली दो तरंगों व्यतिकरण उत्पन्न कर रही है तब परिणामी तीव्रता -
View SolutionStatement-1: Two longitudinal waves given by equation y1(x,t)=2asin(ωt−kx)
and y2(x,t)=asin(2ωt−2kx)
will have equal intensity.
Statement-2 : Intensity of waves of given frequency in same medium is proportional to square of amplitude only.
View SolutionTwo waves are given by y1=asin(ωt−kx) and y2=acos(ωt−kx). The phase difference between the two waves is -
View Solution
