A horizontal stretched string, fixed at two ends, is vibrating in its fifth harmonic according to the equation, y(x,t)=(0.01m)sin[(62.8m−1x]cos[(628s−1)t]. Assuming p=3.14, the correct statement(s) is (are)Solution in Gujrati
The number of node is 5
The length of the string is 0.25 m
The maximum displacement of the midpoint of the string. From its equilibrium position is 0.01 m
The fundamental frequency is 100 Hz
The correct Answer is:B, C
Step by step video & image solution for A horizontal stretched string, fixed at two ends, is vibrating in its fifth harmonic according to the equation, y(x,t)=(0.01 m) sin[(62.8 m^(-1)x] cos[(628 s^(-1))t]. Assuming p = 3.14, the correct statement(s) is (are) by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Tube A has both ends open while tube B has one closed, otherwise they are identical. The ratio of fundamental frequency of tube AandB is
View SolutionAt absolute zero temperature Si acts as ……..
View SolutionA horizontal stretched string, fixed at two ends, is vibrating in its fifth harmonic according to the equation, t(x,t)=(0.01m)sin[(62.8m−1)t]. Assuming π=3.14, the correct statement (s) is (are)
View SolutionThe equation for the vibration of a string fixed at both ends vibrating in its third harmonic is given by y=2cmsin[(0.6cm−1)x]cos[(500πs−1)t]. The length of the string is
View SolutionA horizontal stretched string, fixed at two ends, is vibrating in its fifth harmonic according to the equation, y(x,t)=(0.01 m) sin[(62.8 m^(-1)x] cos[(628 s^(-1))t] . Assuming p = 3.14 , the correct statement(s) is (are)
View Solutionthe equation for the vibration of a string fixed both ends vibration in its third harmonic is given by
y = 2 cm sin [(0.6cm−1)×]cos[(500ps−1t]
View SolutionA transverse wave of equation y = 2 sin (0.01 x +30 t) moves on a stretched string from one end to another end. In the equation of wave, x and y are in cm and t is in second. The time taken by wave to reach from one end to another end of string is 5 s. The length of string is
View SolutionA horizontal stretched string, fixed at two ends, is vibrating in its fifth harmonic according to the equation, y(x,t)=(0.01m)sin[(628s−1)t]. Assuming π=3.14 , the correct statement(s) is (are) :
View SolutionThe equation of a stationary wave on a string
clamped at both ends and vibrating in its third
harmonic is given by y=0.5sin(0.314x)cos(600πt)
where x and y are in cm and t is in sec. What is the
length of the string?
View Solutionदोनों सिरों पर परिबद्ध क्षैतिज तनित डोरी पाँचवीं गुणवृत्ति समीकरण y(x,t) = (0.01 मी ) sin(62.8मी−1)x]cos[628से−1t] द्वारा संपित हो रही है। यदि π=3.14 , मान जाये तब निम्न प्रकथन सही है / है
View SolutionThe equation of vibration of a 60 cm long string string stretched at both ends is given by y = 4 "sin" (pi x)/(15) "cos" 96 pi t . Here x and y are expressed in cm and t in s . What are the equations of the two superposed waves ?
View Solutionएक तनी हुयी डोरी दो दृढ सिरों पर कसी हुयी है इस पर कम्पन का समीकरण y=cos2πtsin2πx है डोरी की न्यूनतम लम्बाई होती
View SolutionThe Equation for the vibration of a string fixed at both ends vibrating in its third harmonic is given by y=2sin(0.6x)cos(500πt) (x, y are in cm t is in sec). The length of the string is
View SolutionThe equation of a travelling wave on a string is y =(0.10 mm) sin[31.4 m^(-1)x + (314 s^(-1))t]
View Solutionthe equation for the vibration of a string fixed both ends vibration in its third harmonic is given by
y = 2 cm sin [(0.6cm−1x)×]cos[(500ps−1t]What is the position of node?
View SolutionA string of length 1 m fixed at one end and on the other end a block of mass M =4 kg is suspended. The string is set into vibrations and represented by equation y=6sin(πx10).cos100πt where x and y are in cm and t in seconds.
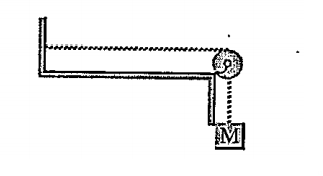
Calculate maximum kinetic energy of the string.
View Solution
