A string of length 1 m fixed at one end and on the other end a block of mass M =4 kg is suspended. The string is set into vibrations and represented by equation y=6sin(πx10).cos100πt where x and y are in cm and t in seconds.
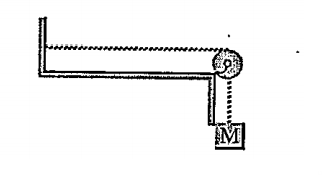
Calculate maximum kinetic energy of the string.
142.12 joule
Topper's Solved these Questions
Similar Questions
A string of length 1 m fixed one end and on the other end a block of mass M=4kg is suspended. The string is set into vibration and represented by equation y=6sin(πx10)cos(100πt) where x and y are in cm and t is in seconds.
(i) Find the number of loops formed in the string.
(ii) Find the maximum displacement of a point at x=5/3cm
(iii) Calculate the maximum kinetic energy of the string.
_E01_141_Q01.png) .
.
View SolutionA string of length 1 m fixed one end and on the other end a block of mass M=4kg is suspended. The string is set into vibration and represented by equation y=6sin(πx10)cos(100πt) where x and y are in cm and t is in seconds.
(i) Find the number of loops formed in the string.
(ii) Find the maximum displacement of a point at x=5/3cm
(iii) Calculate the maximum kinetic energy of the string.
(iv) Write down the equations of the component waves whose superposition given the wave.
_E01_141_Q01.png) .
.
View Solution
Knowledge Check
The vibrations of a string of length 600cm fixed at both ends are represented by the equation y=4sin(πx15)cos(96πt)
where x and y are in cm and t in seconds.AThe maximum displacement of a particle at x=5cm is 2√3cm.BThe nodes located along the string are 15n where ineger n varies from 0 to 40.CThe velocity of the particle at x=7.5cm at t=0.25sec is zeroDThe equations of the component waves whose superpostion gives the above wave are 2sin2π(x30+48t),2sin2π(x30−48t)In the arrangement shown in Fig. 7.100 , mass can be hung from a string with a linear mass density of 2×10−3kg/m that passes over a light pulley . The string is connected to a vibrator of frequency 700Hz and the length of the string between the vibrator and the pulley is 1m.

The string is set into vibrations and represented by the equation y=6sin(πx10)cmcos(14×103πt) where x ane y are in cm , and t in s, the maximum displacement at x=5m from the vibrator isA6cmB3cmC5cmD2cmThe vibrations of a string of length 60 cm fixed at both ends are represented by the equation
y=4sin(πx/15)cos(96πt)
where x and y are in cm and t in seconds. The maximum displacement at x = 5 cm is–A2√3cmB3√2cmC√2cmD√3cm
In the arrangement shown in Fig. 7.100 , mass can be hung from a string with a linear mass density of 2×10−3kg/m that passes over a light pulley . The string is connected to a vibrator of frequency 700Hz and the length of the string between the vibrator and the pulley is 1m.

The string is set into vibrations and represented by the equation y=6sin(πx10)cmcos(14×103πt) where x ane y are in cm , and t in s, the maximum displacement at x=5m from the vibrator is
View SolutionThe vibrations of a string of length 60cm fixed at both cnds are represented by the equation.
y=4sin(πx/(15))cos(96πt), where x and y are in cm and t in second. The maximum displacement (in cm ) at x= 52 (cm) is
View SolutionThe vibrations of a string fixed at both ends are represented by y=16sin(πx15)cos96πt where x and y are in cm and t in seconds. Then the phase difference between the points at x = 13 cm and X = 16 cm in radian is
View SolutionThe vibrations of string of length 60cm fixed at both ends are presented by the equations
y=4sin(πx/15)cos(96πt)
where xandy are in cm and t in s. The maximum displacement at x=5cm is
View SolutionThe vibrations of a string fixed at both ends are represented by y=16sin(πx15)cos(96πt). Where 'x' and 'y' are in cm and 't' in seconds. Then the phase difference between the points at x=13cm and x=16 in radian is
View Solution
