A thin rod of length 6 m is lying along the x-axis with its ends at x=0 and x=6m. Its linear density *mass/length ) varies with x as kx4. Find the position of centre of mass of rod in meters. Solution in Gujrati
5m
3m
2m
4m
The correct Answer is:A
xcm=∫xdm∫dm=∫60x(kx4dx)∫60(kx4dx)=∫60x5dx∫60x4dx=(x66)6(x55)60=5m
Topper's Solved these Questions
- TEST PAPERSBOOK - ALLEN CHAPTER - TEST PAPERSEXERCISE - PAPER 2
60 Videos
- TEST PAPERSBOOK - ALLEN CHAPTER - TEST PAPERSEXERCISE - PAPER 3
92 Videos
- TEST PAPER 4BOOK - ALLEN CHAPTER - TEST PAPER 4EXERCISE - PHYSICS
45 Videos
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR BOOK - ALLEN CHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (J-A)
7 Videos
Similar Questions
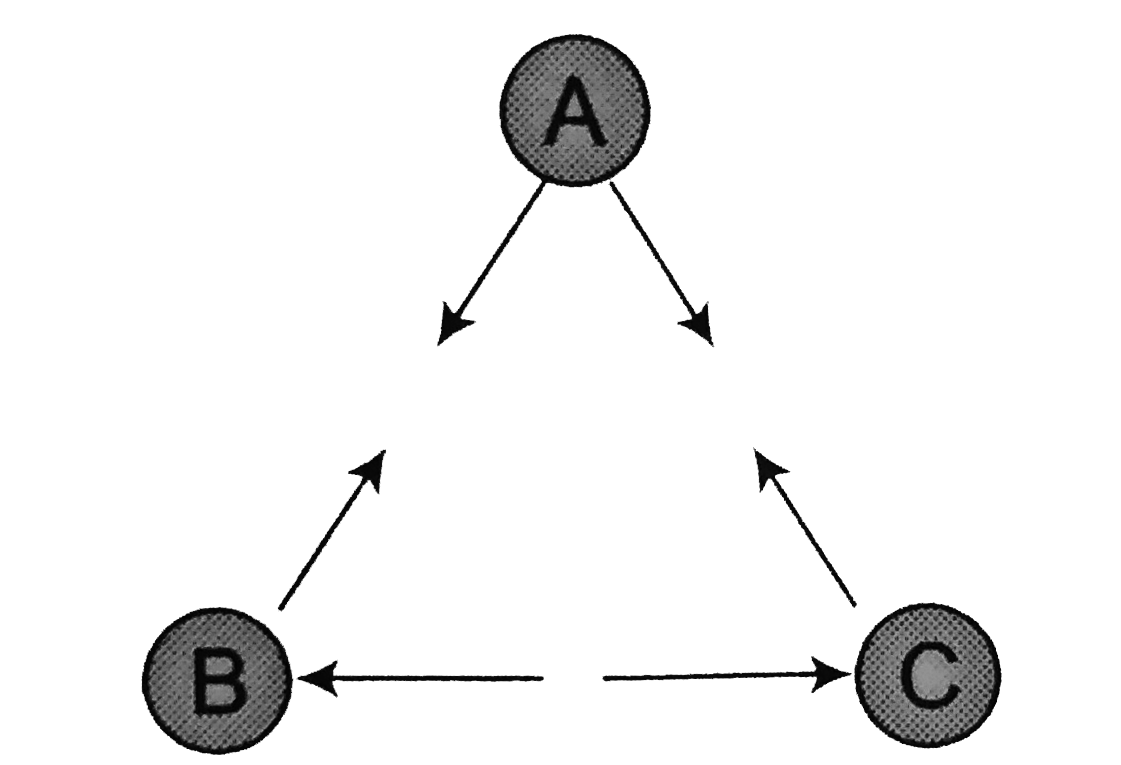
The diagram shows the arrangement of three small uniformally charged spheres, A,B and C. The arrow indicate the direction of the electrostatic forces acting between the spheres (for example, the left arrow on sphere A indicates the electronstatic force on sphere A due to sphere B). At least two of the spheres are positively charged. Which sphere, if any, could be negatively charged?
View SolutionA satellite S is moving in an elliptical orbit around the earth. The mass of the satellite is very small compared to the mass of the earth.
View SolutionTwo forces, each of magnitude F have a resultant of the same magnitude F. The angle between the two forces is
View SolutionMatch List I with List II and select the correct answer using the codes given below the lists :

View SolutionA rod of length L is placed along the x-axis between x=0 and x=L . The linear mass density (mass/length) rho of the rod varies with the distance x from the origin as rho=a+bx . Here, a and b are constants. Find the position of centre of mass of this rod.
View SolutionA non-uniform thin rod of length L is palced along X-axis so that one of its ends is at the origin. The linear mass density of rod is lambda = lambda_(0)x . The centre of mass of rod divides the length of the rod in the ratio:
View SolutionA rod of length L is placed along the x-axis between x = 0 and x = L. The linear density (mass/length) lamda of the rod varies with the distance x from the origin as lamda = Rx. Here, R is a positive constant. Find the position of centre of mass of this rod.
View SolutionA rod of length L is placed along the x-axis between x = 0 and x = L. The linear density (mass/ length) lambda of the rod varies with the distance x from the origin as lambda = Rx . Here, R is a positive constant. Find the position of centre of mass of this rod.
View SolutionA non–uniform thin rod of length L is placed along x-axis as such its one of ends at the origin. The linear mass density of rod is lambda=lambda_(0)x . The distance of centre of mass of rod from the origin is :
View SolutionIf the linear density of a rod of length L varies as lambda = A+Bx , find the position of its centre of mass .
View SolutionIf the linear density of a rod of length L varies as lambda = (kx^(2))/(L) where k is a constant and x is the distance of any point from one end, then find the distance of centre of mass from the end at x = 0.
View SolutionA rod of length L is placed along the x -axis between x = 0 and x = L. The linear density (mass/length) ρ of the rod varies with the distance x from the origin as ρ=a+bx . Here a and b are constants. Find the position of centre of mass of this rod.

View SolutionIf the linear density of a rod of length L varies as λ=A+Bx, find the position of its centre of mass.
View SolutionIf the linear density of a rod of length L varies as lamda=(kx^(2))/(L) where k is a constant and x is the distance of any point from one end, then find the distance of centre of mass from the end at x=0.
View SolutionIf the linear density of a rod of length L varies as lambda=A+Bx , find the position of its centre of mass.
View SolutionIf the linear density of a rod of length L varies as lambda=(kx^(2))/(L) where k is a constant and x is the distance of any point from one end, then find the distance of centre of mass from the end at x=0 .
View Solution
