n moles of an ideal triatomic linear gas undergoes a process in which the temperature changes with volume as 'T'=K1V2 where k1 is a constant. Choose incorrect alternative. Solution in Gujrati
At normal temperature Cv=52R
At any temperature Cp−Cv=R
At normal temperature molar heat capacity C=3R
At any temperature molar heat capacity C=3R
The correct Answer is:C
At normal temperature Cv=f2R=52R, At any
temperature Cv−Cv=(f2+1)−f2r=R
from process T=K1V2& ideal gas equation PV =nRT
we have PV−1= constant ⇒x=−1
⇒C=Cv+R1−x=Cv+R1+1=Cv+R2
At normal temperature C=52R+52=3R
Topper's Solved these Questions
- TEST PAPERSBOOK - ALLEN CHAPTER - TEST PAPERSEXERCISE - Part-1 Physics
15 Videos
- TEST PAPERSBOOK - ALLEN CHAPTER - TEST PAPERSEXERCISE - part-2 physics
73 Videos
- TEST PAPERSBOOK - ALLEN CHAPTER - TEST PAPERSEXERCISE - PAPER 2
60 Videos
- TEST PAPER 4BOOK - ALLEN CHAPTER - TEST PAPER 4EXERCISE - PHYSICS
45 Videos
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR BOOK - ALLEN CHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (J-A)
7 Videos
Similar Questions
A quantity of 2 mole of helium gas undergoes a thermodynamic process, in which molar specific heat capacity of the gas depends on absolute temperatureT , according to relation:
C=3RT4T0
where T0 is initial temperature of gas. It is observed that when temperature is increased. volume of gas first decrease then increase. The total work done on the gas until it reaches minimum volume is :-
View SolutionA bead is connected with a fixed disc of radius R by an inextensible massless string in a smooth horizontal plane. If the bead is pushed with a velocity v0 prependicular to the string, the bead moves in a curve and consequently collapses on the disc. Then

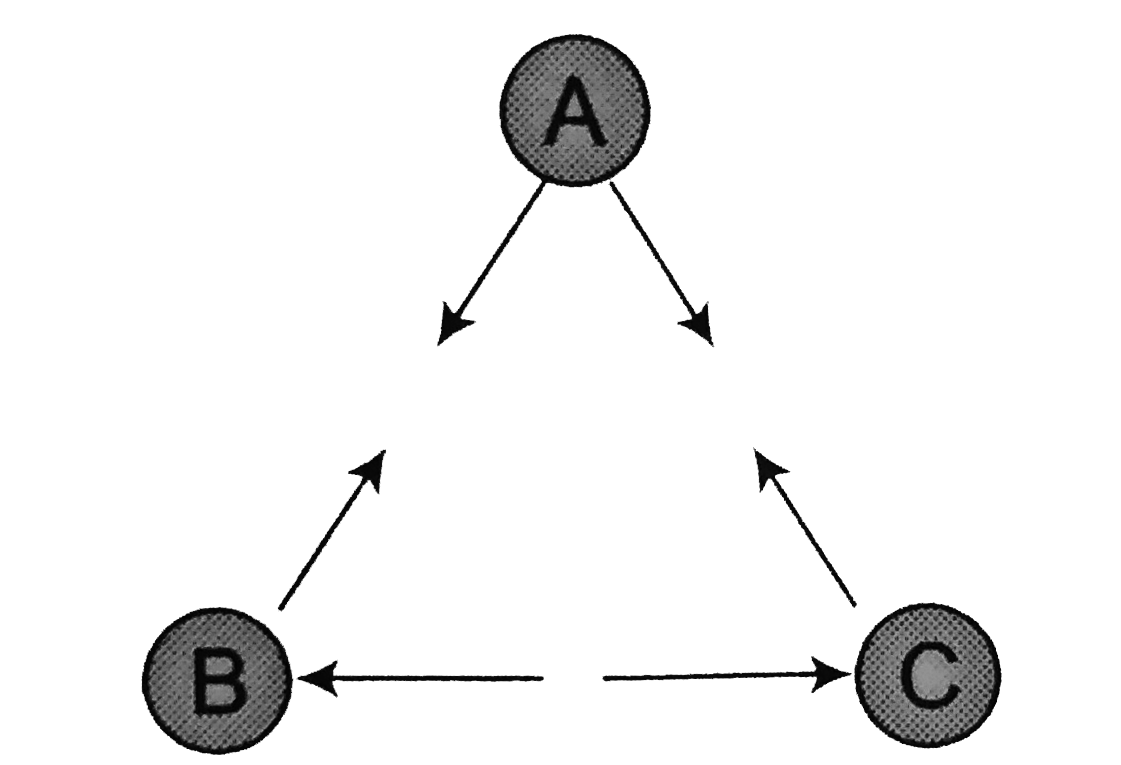
View SolutionThe diagram shows the arrangement of three small uniformally charged spheres, A,B and C. The arrow indicate the direction of the electrostatic forces acting between the spheres (for example, the left arrow on sphere A indicates the electronstatic force on sphere A due to sphere B). At least two of the spheres are positively charged. Which sphere, if any, could be negatively charged?
View SolutionTwo forces, each of magnitude F have a resultant of the same magnitude F. The angle between the two forces is
View SolutionMatch List I with List II and select the correct answer using the codes given below the lists :

View SolutionOne mole of an ideal gas undergoes a process P=P0[1+(2V0V)2]−1, where P0V0 are constants. Change in temperature of the gas when volume is changed from V=V0→V=2V0 is:
View SolutionOne mole of an ideal gas goes through a process in which the entropy of the gas changes with temperature T as S = aT + C_V 1n T , where a is a positive constant. C_V is the molar heat capacity of this gas at constant volume. Find the volume dependence of the gas temperature in this process if T = T_0 at V = V_0 .
View Solutionn moles of an ideal gas undergo a process in which the temperature changes with volume as T=kv^(2) . The work done by the gas as the temperature changes from 7_(0) to 47_(0) is
View SolutionA certain amount of an ideal monoatomic gas undergoes a thermodynamic process such that VT^(2)= constat where V= volume of gas, T= temperature of gas. Then under process
View SolutionOne mole of an ideal monatomic gas undergoes a linear process from A to B , in which is pressure P and its volume V change as shown in figure .
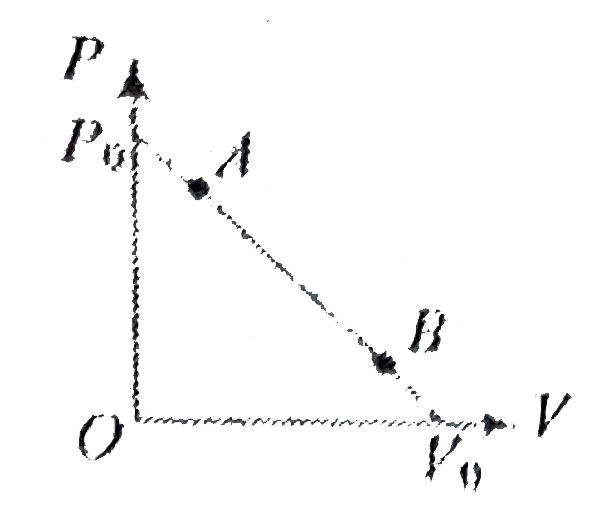
The absolute temperature T versus volume V for the given process is
View SolutionOne mole of ideal gas undergoes a linear process as shown in figure below. Its temperature expressed as function of volume V is -

View SolutionOne mole of an ideal monotomic gas undergoes a linear process from A to B in which its pressure p and its volume V change as shown in figure.
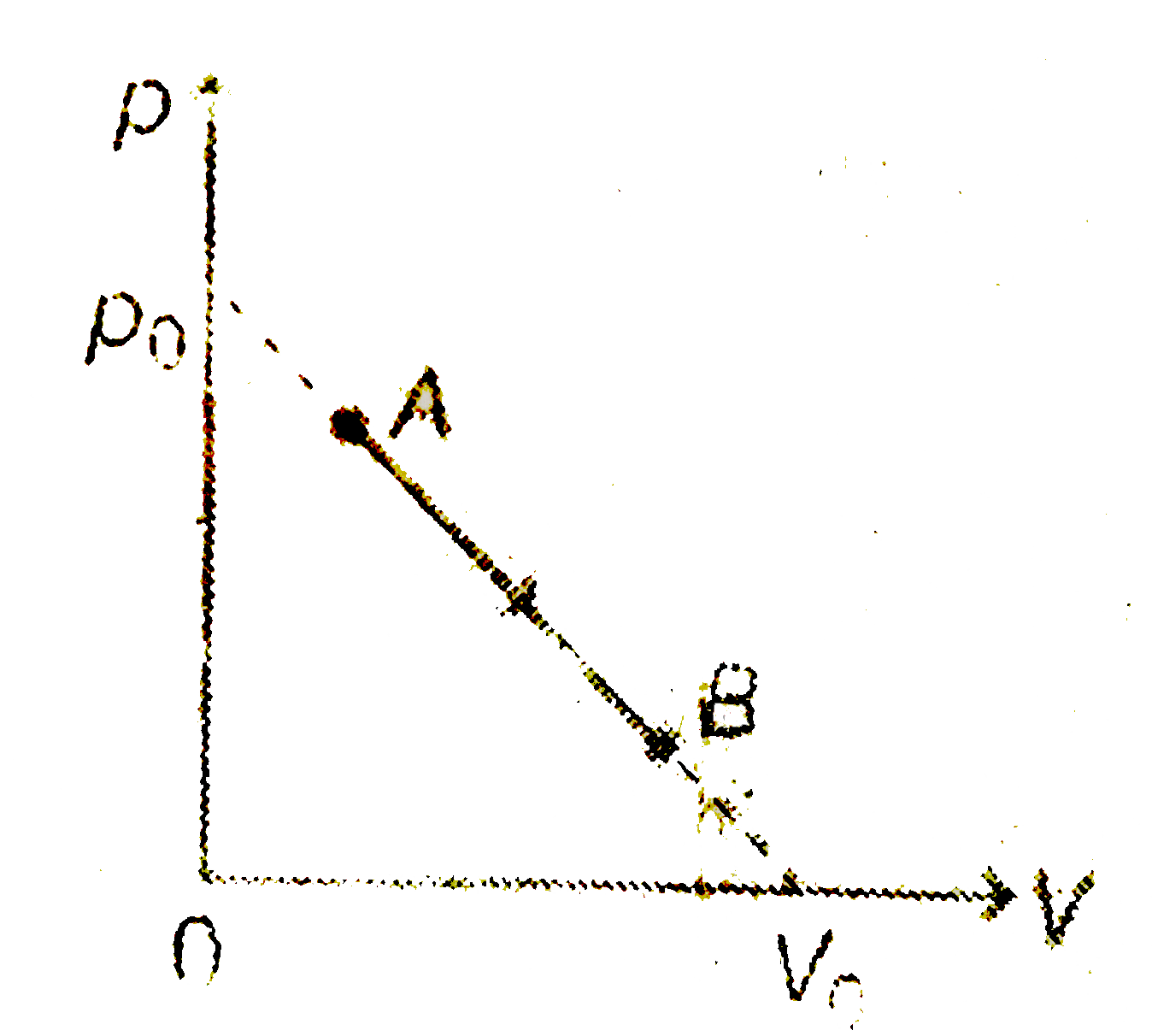
The absolute temperature T versus volume V for the given process is
View SolutionOne mole of a monatomic ideal gas undergoes a cyclic process as shown in the figure (where V is the volume and T is the temperature). Which of the statements below is (are) true ?
View SolutionOne mole of a monatomic ideal gas undergoes a cyclic process as shown in the figure (where V is the volume and T is the temperature). Which of the statements below is (are) true?
View SolutionFor a monatomic ideal gas undergoing an adiabatic change, the relation between temperature and volume is T V^(x) = constant where x is:
View SolutionA monatomic gas undergoes a thermodynamic process such that T∝V−27 (T = temperature and V = volume of the gas) As heat is supplied to the gas, choose INCORRECT option.
View Solution
