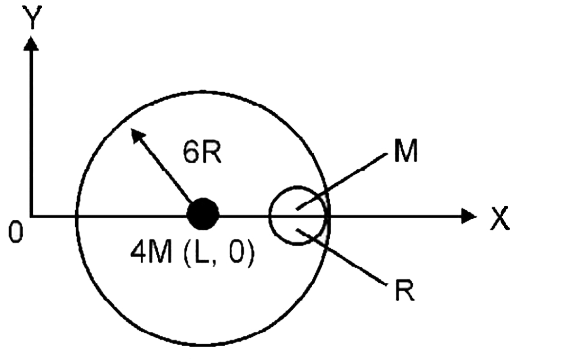
A small sphere of radius R is held against the inner surface of a larger sphere of radius 6R. The masses of large and small spheres are 4M and M, respectively , this arrangement is placed on a horizontal table. There is no friction between any surfaces of contact. The small sphere is now released. Find the coordinates of the centre of the larger sphere when the smaller sphere reaches the other extreme position.
 Solution in Gujrati
Solution in Gujrati
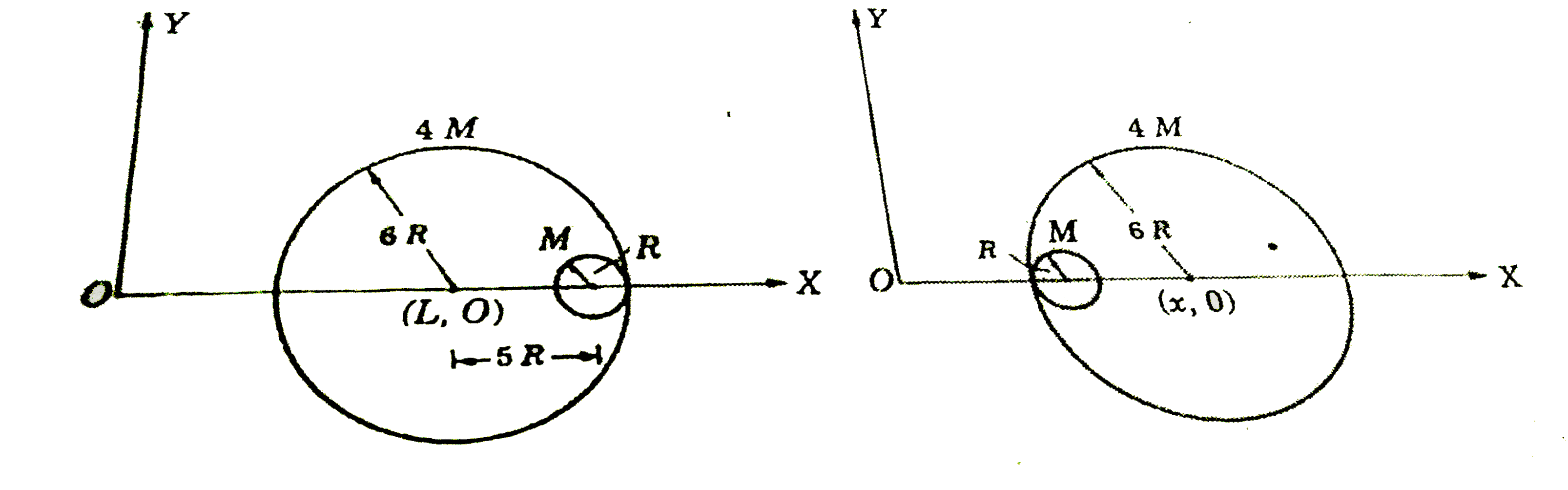
The correct Answer is:(L+2R,0)
xcm=4ML+M(L+5R)5M=4MX+M(X−5R)5M
⇒x=L+2R

Topper's Solved these Questions
- CENTRE OF MASSBOOK - ALLEN CHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-IV B
14 Videos
- CENTRE OF MASSBOOK - ALLEN CHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-V A
20 Videos
- CENTRE OF MASSBOOK - ALLEN CHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-III
41 Videos
- BASIC MATHEMATICS USED IN PHYSICS &VECTORS BOOK - ALLEN CHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - EXERCISE-IV ASSERTION & REASON
11 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLEN CHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 B (Integer Type Questions)
3 Videos
Similar Questions
A bullet of mass M is fired with a velocity 50m/s at an angle with the horizontal. At the highest point of its trajectory, it collides head-on with a bob of mass 3M suspended by a massless string of length 10/3 metres and gets embeded in the bob. After the collision, the string moves through an angle of 120∘. Find
(i) the angle θ,
(ii) the vertical and horizontal coordinates of the initial position of the bob with respect to the point of firing of the bullet. Take g=10m/s2
View SolutionTwo identical particles move towards each other with velocity 2v and v respectively. The velocity of centre of mass is
View SolutionA particle of mass m, kinetic energy K and momentum p collision head on elastically with another particle of mass 2m at rest. After collision. :
Column IColumn II(A)Momentum of first particle(p)3/4p(B)Momentum of second particle(q)−K/9(C)Kinetic energy of first particle(r)−p/3(D)Kinetic energy of second particle(s)8K9None
View SolutionAssertion: If the initial and final positions coincide, the displacement is a null vector.
Reason: A physical quantity can not be called a vector, if its magnitude is zero.
View SolutionTwo soap bubbles A and B are kept in a closed chamber where the air is maintained at pressure 8N/m2.The radii of bubbles A and B are 2cm and 4cm, respectively. Surface tension of the soap-water used to make bubbles is 0.04N/m. Find tha ratio nB/nA, where nA and nB are the number of moles of air in bubbles A and B, respectively. [Neglect the effect of gravity.]
View SolutionA small sphere of radius R is held against the inner surface of a larger sphere of radius 6R. The masses of large and small spheres are 4M and M, respectively , this arrangement is placed on a horizontal table. There is no friction between any surfaces of contact. The small sphere is now released. Find the coordinates of the centre of the larger sphere when the smaller sphere reaches the other extreme position.
View SolutionA small sphere of radius R is held against the inner surface of larger sphere of radius 6R (as shown in figure). The masses of large and small spheres are 4M and M respectivley. This arrangement is placed on a horizontal table. There is no friction between any surfaces of contact. The small sphere is now released. Find the coordinates of the centre of the large spheres, when the smaller sphere reaches the other extreme position.

View SolutionA large insulated sphere of radius r charged with Q units of electricity is placed in contact with a small insulated uncharged sphere of radius r' and is then separated. The charge on the smaller sphere will now be.
View SolutionA small sphere of radius R is held against the inner surface of α larger sphere of radius 6R. The masses of large and small spheres are 4M and M, respectively. This arrangement is placed on a horizontal table. There is no friction between any surfaces of contact. The small sphere is now released. find the co-ordinations of the centre of the larger sphere when the smaller sphere reaches the other extreme position.
View SolutionConsider eight small spheres , radius = r_(s) arranged at the corner of the cube , they are small enough so that they are not in contact . Now place a larger sphere , radius = r_(l) at the centre of the cube . This sphere is just large enough so that it is in contact with the eight small sphere . Now let the radius of the large sphere shrink , but keep the small sphere in contact with it . what is the radius ratio r_(s)//r_(l) , when the small spheres at the cube corners come in to contact with each other .
View SolutionA sphere of mass M and radius R is held on the inner wall of a hollow sphere of mass 4M and radius 6R .The bigger sphere is kept on a smooth horizontal table and the centres of the two spheres lie on horizontal line.The system of two spheres is released from this position. The smaller sphere slides on the inner smooth wall to reach the other extreme position (shown in dotted line).The displacement of the centre of the larger sphere as the smaller sphere moves from one extreme to another is xcm. Value of x is: ( Take R=4.5cm) qquad y qquad yR Delta M
View SolutionA small sphere of radius R is kept attached to the smooth inner wall of a hollow sphere of radius 6 R Fig. The system is kept on a frictionless horizontal table. On releasing the small sphere, as it reaches the other end of the diameter, what will be the coordinates of the centre of the large sphere? Masses of the small and large sphere are M and 4M respectively.
View Solutionஒரு உலோகக்கோளம் உருக்கப்பட்டு சிறிய கோளங்களை செய்யப்படுகிறது. ஒவ்வொரு சிறிய கோளத்தின் ஆரமும் பெரிய கோளத்தின் ஆரத்தில் நான்கில் 1பங்கு எனில் எத்தனை சிறிய கோளங்கள் செய்ய முடியும்?
View SolutionA solid metallic sphere of radius 8 cm is melted to form 64 equal small solid spheres . The ratio of the surface area of this sphere to that of a small sphere is
View SolutionA small sphere of radius R is held against the inner surface of larger sphere of radius 6R (as shown in figure). The masses of large and small spheres are 4M and M respectively. This arrangement is placed on a horizontal table. There is no friction between any surfaces of contact. The small sphere is now released. Find the coordinates of the centre of the large spheres, when the smaller sphere reaches the other extreme position.
View Solution
