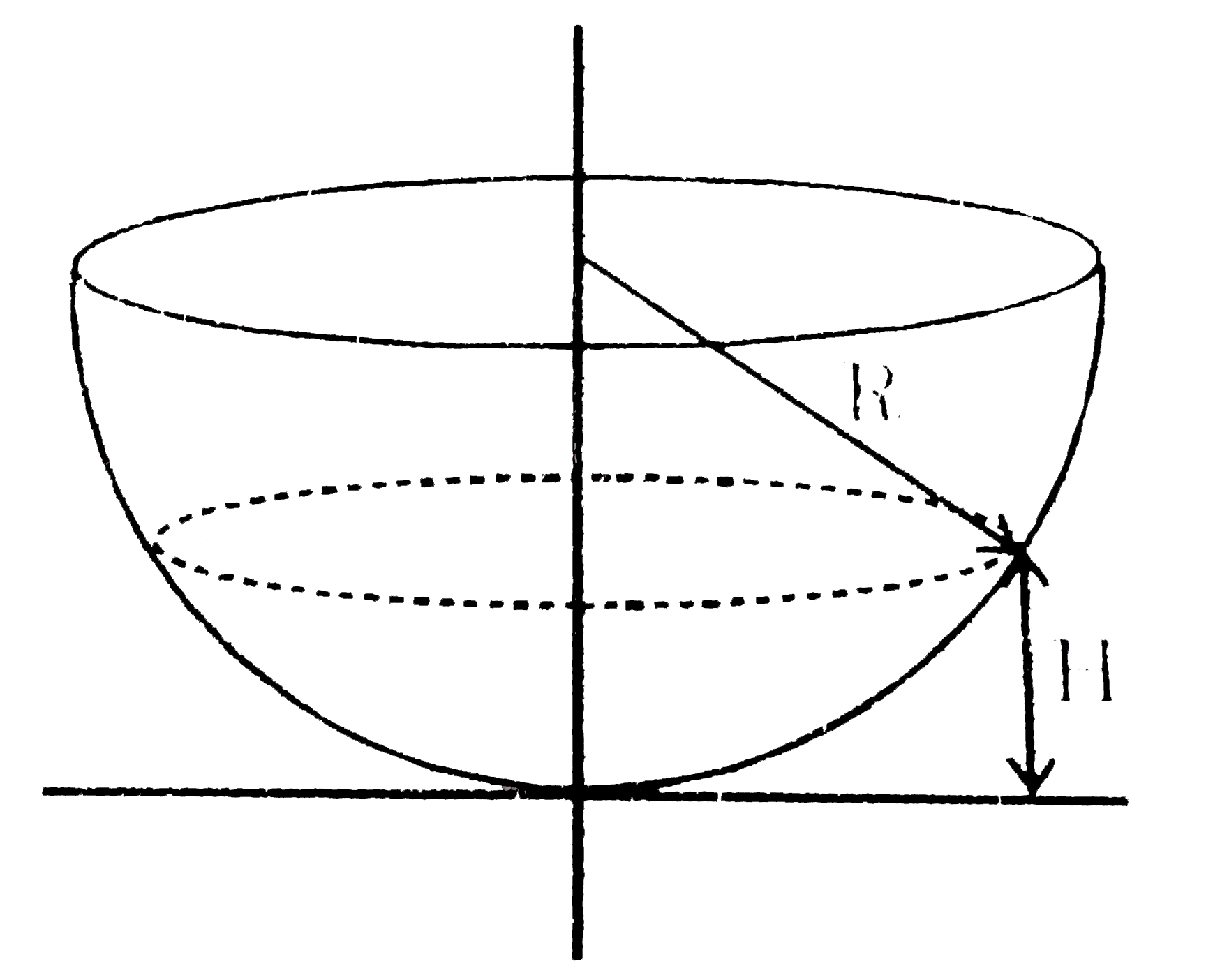
A small marble of mass m moves in a circular orbit very close to the bottom of a circular bowl. Assume that the marble can only move in orbits whose angular momentum is $L = \frac{n h}{2 π}$ where h is plank constant.
Solution in Gujrati

A

(a)The allowed radius of the circular orbit is proportionsl to $n (3 / 2)$

B

(b)The allowed speed is proportional to $n (1 / 2)$

C

(c) Taking gravitional potential energy at bottom to be zero, the allowed energy is given by $\frac{n h}{2 π} \sqrt{\frac{g}{R}}$

D

(d)Gravotational potential energy and kinetic energy in any allowed state are equal (taking reference at bottom.)

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B, C, D

$N cos θ = m g$
$N sin θ = \frac{m v^{2}}{x}$

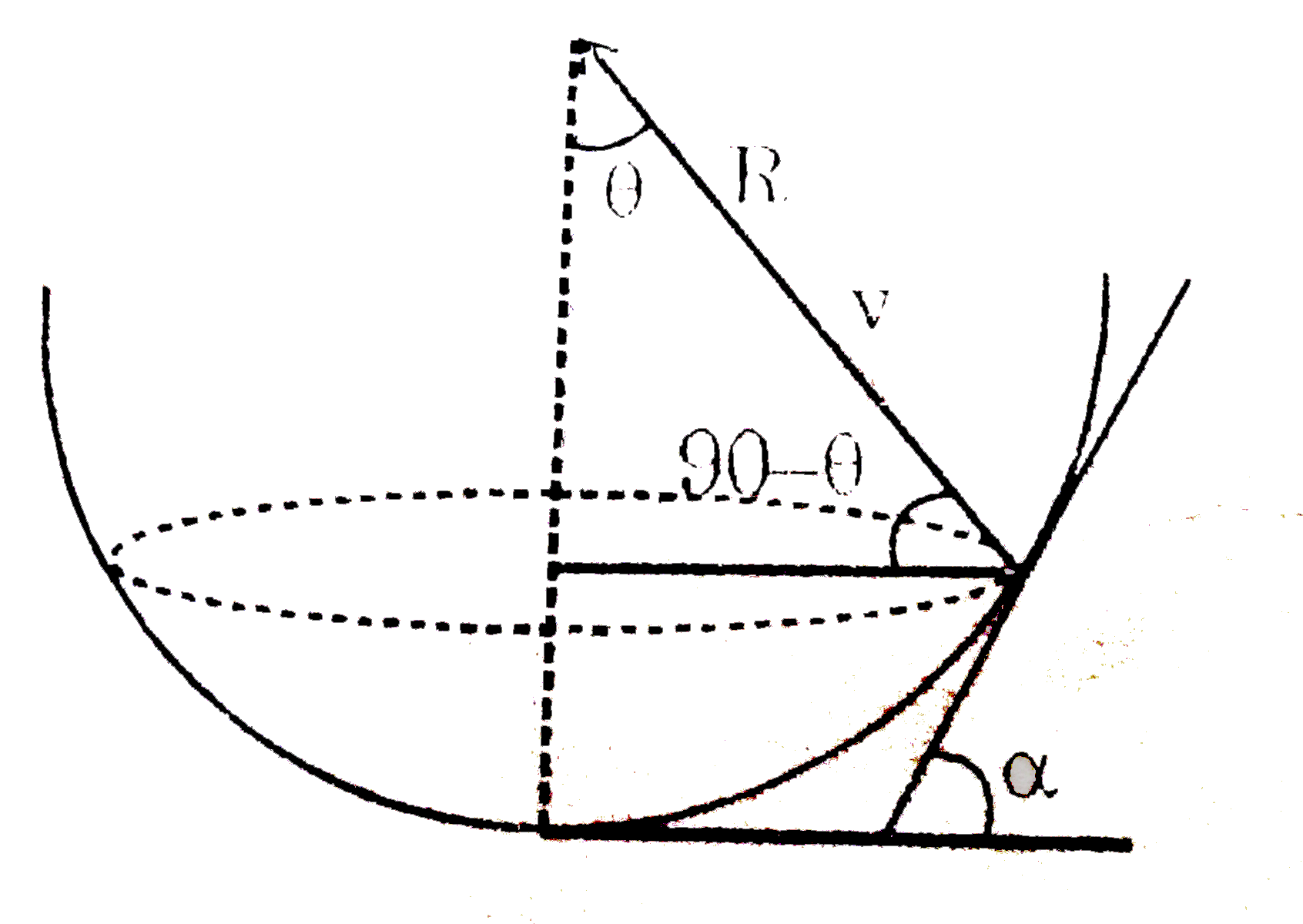
$tan θ = \frac{v^{2}}{g x} = \frac{v^{2}}{g R sin θ}$
$m v x = \frac{n h}{2 π}$
$m v \times R sin θ = \frac{n h}{2 π}$
$m \sqrt{\frac{g R {sin}^{2} θ}{cos θ}} R sin θ = \frac{n h}{2 π}$
$m \sqrt{g R^{3}} \frac{{sin}^{2} θ}{\sqrt{cos θ}} = \frac{n h}{2 π}$
$cos θ \approx 1$
$m \sqrt{g R^{3}} \times \frac{x^{2}}{R^{2}} = \frac{n h}{2 π}$
$x = \sqrt{\frac{n h}{2 π m} \sqrt{\frac{R}{g}}}$
$v \propto \sqrt{n}$
$v = \frac{\sqrt{n h}}{\sqrt{2 π \sqrt{m}}} \times \sqrt{\frac{n h}{2 π m} \sqrt{\frac{R}{g}}} = \sqrt{\frac{n h}{2 π m} \sqrt{\frac{g}{R}}}$
$E = m g h + \frac{1}{2} m v^{2}$
$m g (R - R cos θ) + \frac{1}{2} m \times \frac{n h}{2 π m} \sqrt{\frac{g}{R}}$
$\frac{1}{2} m g R \times \frac{x^{2}}{R^{2}} + \frac{1}{2} \frac{n h}{4 π} \sqrt{\frac{g}{R}}$
$\frac{m g}{2 R} \times \frac{n h}{2 π m} \sqrt{\frac{R}{g}} + \frac{n h}{4 π} \sqrt{\frac{g}{R}}$
$E = \frac{n h}{2 π} \sqrt{\frac{g}{R}}$

|

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

ALLEN -TEST PAPERS-Part-1 Physics

Home
Ask Doubt
Profile