From a water tap, liquid comes out from cylinder. As water moves down, radius of that cylinder decreases. Consider, a very small element of height h and radius R (due to small height radius is assumed to be constant)

This element is given in the diagram. An imaginary cross-section ABCD divides this element in two equal semi cylinder. S is surface tensionof liquid. Now choose correct statement(s)
 Solution in Gujrati
Solution in Gujrati
Surface energy of this elementary cylinder is S[2πRh+2πR2]
Pressure inside the cylinder is more than atmospheric pressure by2SR
Force exerted by one half cylinder on another half cylinder due to surface tension is 2Sh.
Surface energy of this elementary cylinder is S×2πRh
The correct Answer is:C, D
Surface energy=free surface area×surface tension
for a cylindrical surface excess pressure is SR
Topper's Solved these Questions
- TEST PAPERSBOOK - ALLEN CHAPTER - TEST PAPERSEXERCISE - part-2 physic
48 Videos
- TEST PAPERSBOOK - ALLEN CHAPTER - TEST PAPERSEXERCISE - PHYSICS
16 Videos
- TEST PAPERSBOOK - ALLEN CHAPTER - TEST PAPERSEXERCISE - Part-1 Physics
15 Videos
- TEST PAPER 4BOOK - ALLEN CHAPTER - TEST PAPER 4EXERCISE - PHYSICS
45 Videos
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR BOOK - ALLEN CHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (J-A)
7 Videos
Similar Questions
In a continuous printing process paper is drawn into the press at a constant speed v. Denoting by 'r' the radius of the paper roll at any given time and by 'b' the thickness of the paper. What is the angular acceleraion of the paper roll?

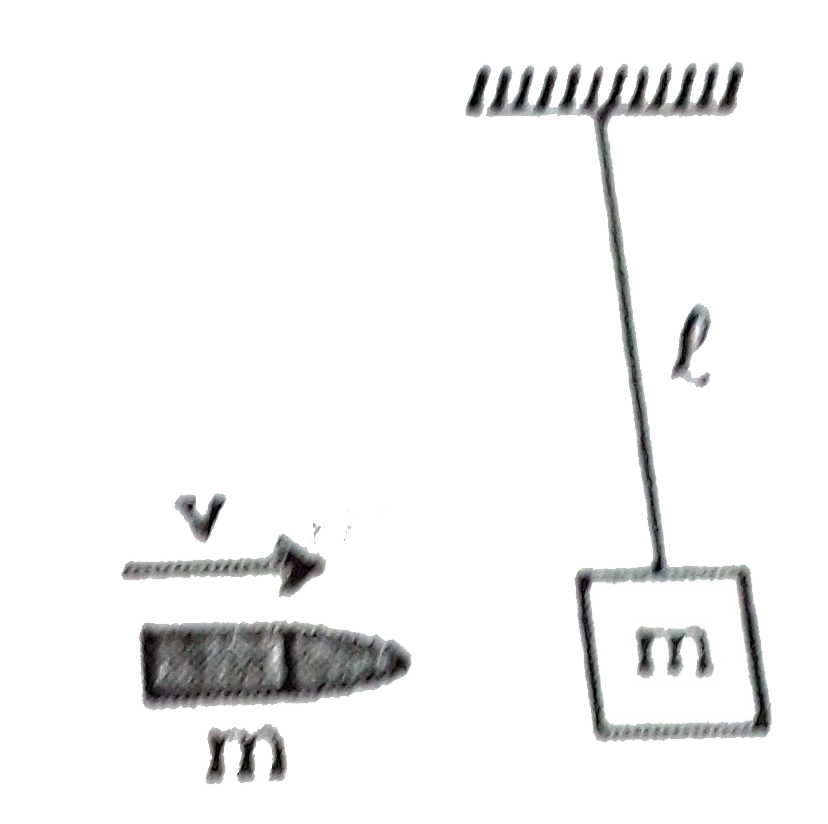
View SolutionA block of mass m is hanging from a light string of length l . A bullet of mass m strikes the hanging mass and gets embedded into it. The value of v such that tension in string and the speed of combined mass becomes zero simultaneously during the subsequent motion , is :-
View SolutionA quantity of 2 mole of helium gas undergoes a thermodynamic process, in which molar specific heat capacity of the gas depends on absolute temperatureT , according to relation:
C=3RT4T0
where T0 is initial temperature of gas. It is observed that when temperature is increased. volume of gas first decrease then increase. The total work done on the gas until it reaches minimum volume is :-
View SolutionTwo forces, each of magnitude F have a resultant of the same magnitude F. The angle between the two forces is
View SolutionMatch List I with List II and select the correct answer using the codes given below the lists :

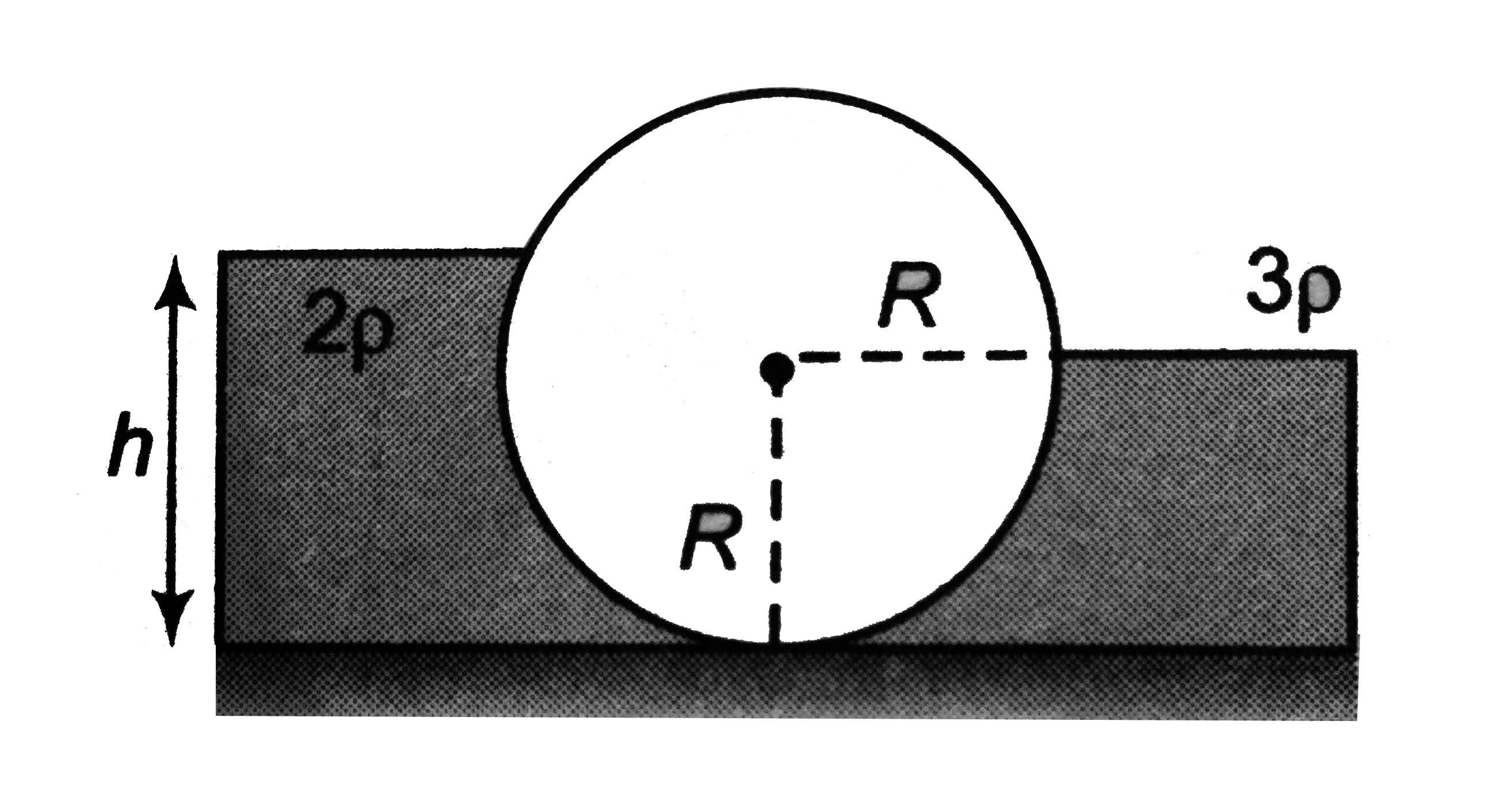
View SolutionIn the figure shown, the heavy cylinder (radius R) reasting on a smooth surface separates two liquids of densities 2ρ and 3ρ. The height h for the equilibrium of cylinder must be
View SolutionA cylindrical container of radius 'R' and height 'h' is completely filled with a liquid. Two horizontal L-shaped pipes of small cross-sectional area 'a' are connected to the cylinder as shown in the figure. Now the two pipes are opened and fluid starts coming out of the pipes horizontally in opposite directions. Then the torque due to ejected liquid on the system is

View SolutionWater is filled to height h in a fixed vertical cylinder placed on horizontal surface. At time t = 0 a small hole a drilled at a height h//4 from bottom of cylinder as shown. The cross section area of hole is a and the cross-section area of cylinder is A such that A gtgt a . Let the value of horizontal distance of point where the4 water fall on horizontal surface from bottom of cylinder be x as shown. Then from time t = 0 till water comes out of hole, pick the correct statement:
View SolutionWater is filled to height h in a fixed vertical cylinder placed on horizontal surface. At time t = 0 a small hole a drilled at a height h//4 from bottom of cylinder as shown. The cross section area of hole is a and the cross-section area of cylinder is A such that A gtgt a . The duration of time for which water flows out of hole is.
View SolutionFrame the formula: The lateral surface area of a cylinder S is equal to twice the product of π, radius (r) and height (h) of the cylinder.
View SolutionA conical portion of radius R and height H is removed from the bottom of a cylinder of radius R. The volume of the remaining cylinder is V and its mass is M. It is suspended by a string in a liquid of density ρ where it stays vertical . The upper surface of the cylinder is at depth h below the liquid surface . The force on the bottom of the cylinder by the liquid is

View SolutionThe lateral surface of a cylinder is equal to the curved surface of a come. If the radius be the same, find the ratio of the height of the cylinder and slant height of the cone.
View SolutionA cylinder contains a liquid upto a height 2.5 m . If now a small hole is made at bottom . Liquid comes out with a velocity
View SolutionThe lateral surface of a cylinder is equal to the curved surface of a come. If the radius be the same, find the ratio of the height of the cylinder and slant height of the cone.
View SolutionIn the figure shown, the heavy cylinder (radius R) reasting on a smooth surface separates two liquids of densities 2rho and 3rho . The height h for the equilibrium of cylinder must be
View Solutionएक बेलन जिसकी त्रिज्या =r और ऊँचाई = h है, का वक्र पृष्ठीय क्षेत्रफल है-
View Solution
