A cylindrical capacitor with external radius R, internal radius R−d(d<<R), length l and mass M hangs on an insulating cord in a region where there is a homogenous, vertical magnetic field of strength B. It can rotate freely as a whole around its vertical axis, but is constrained, so that it can not move horizontally. The capacitor is charged and there is a voltage difference
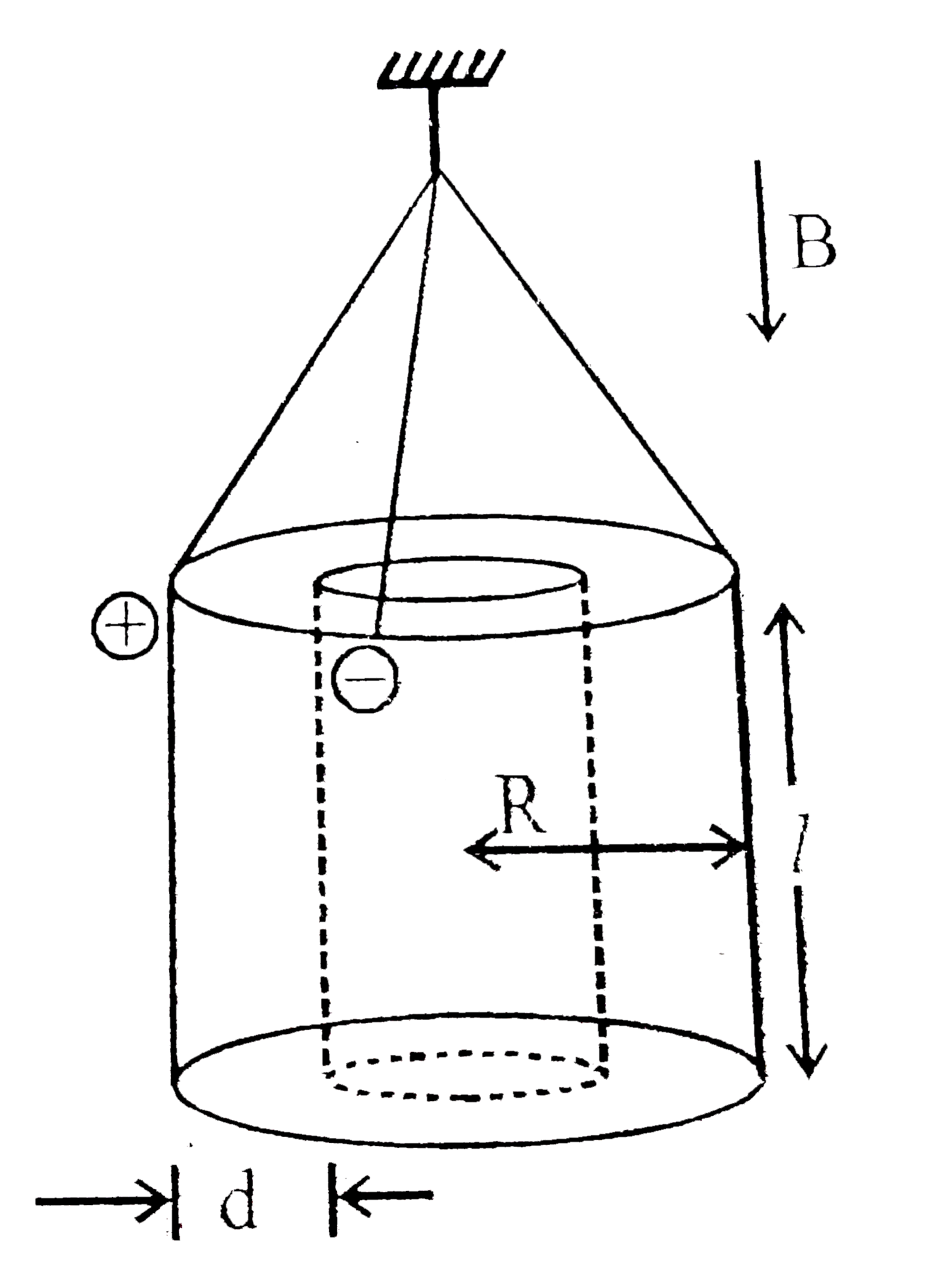
Choose CORRECT statement Solution in Gujrati
When capacitor is discharged through radial wire then value of ωmax depends on values of R and d
Value of ωmax is independent of time dependence of discharge current
Value of ωmax is dependent on time dependence of discharge current
Value of ωmax cannot be calculated with the help of given data.
The correct Answer is:B
Step by step video & image solution for A cylindrical capacitor with external radius R, internal radius R-d(dltltR ), length l and mass M hangs on an insulating cord in a region where there is a homogenous, vertical magnetic field of strength B. It can rotate freely as a whole around its vertical axis, but is constrained, so that it can not move horizontally. The capacitor is charged and there is a voltage difference Choose CORRECT statement by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TEST PAPERSBOOK - ALLEN CHAPTER - TEST PAPERSEXERCISE - part-2 physic
48 Videos
- TEST PAPERSBOOK - ALLEN CHAPTER - TEST PAPERSEXERCISE - PHYSICS
16 Videos
- TEST PAPERSBOOK - ALLEN CHAPTER - TEST PAPERSEXERCISE - Part-1 Physics
15 Videos
- TEST PAPER 4BOOK - ALLEN CHAPTER - TEST PAPER 4EXERCISE - PHYSICS
45 Videos
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR BOOK - ALLEN CHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (J-A)
7 Videos
Similar Questions
In a continuous printing process paper is drawn into the press at a constant speed v. Denoting by 'r' the radius of the paper roll at any given time and by 'b' the thickness of the paper. What is the angular acceleraion of the paper roll?

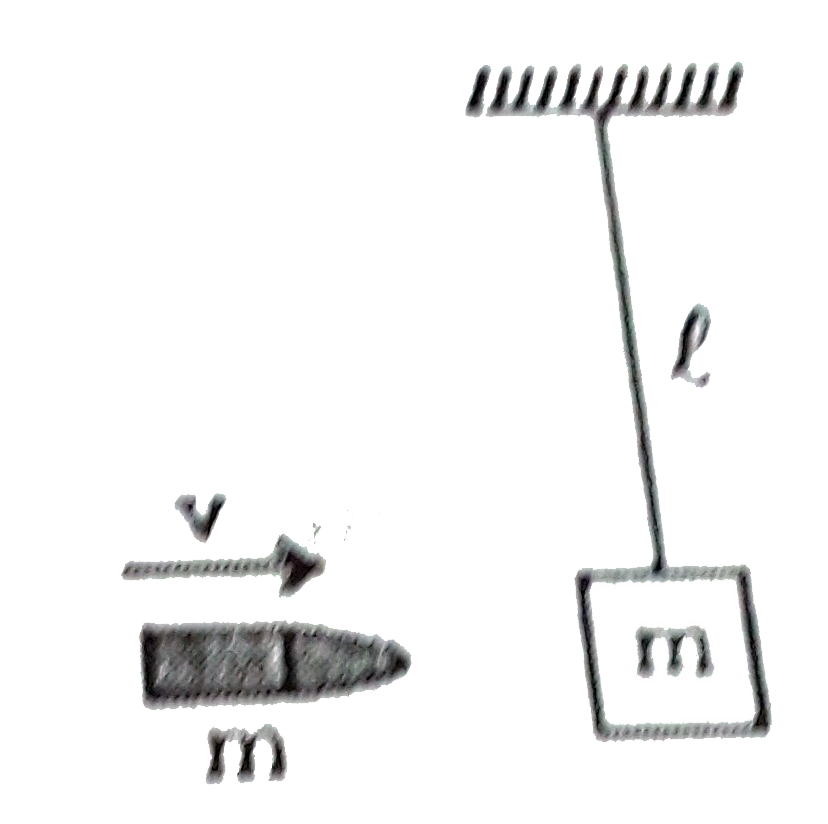
View SolutionA block of mass m is hanging from a light string of length l . A bullet of mass m strikes the hanging mass and gets embedded into it. The value of v such that tension in string and the speed of combined mass becomes zero simultaneously during the subsequent motion , is :-
View SolutionA quantity of 2 mole of helium gas undergoes a thermodynamic process, in which molar specific heat capacity of the gas depends on absolute temperatureT , according to relation:
C=3RT4T0
where T0 is initial temperature of gas. It is observed that when temperature is increased. volume of gas first decrease then increase. The total work done on the gas until it reaches minimum volume is :-
View SolutionTwo forces, each of magnitude F have a resultant of the same magnitude F. The angle between the two forces is
View SolutionMatch List I with List II and select the correct answer using the codes given below the lists :

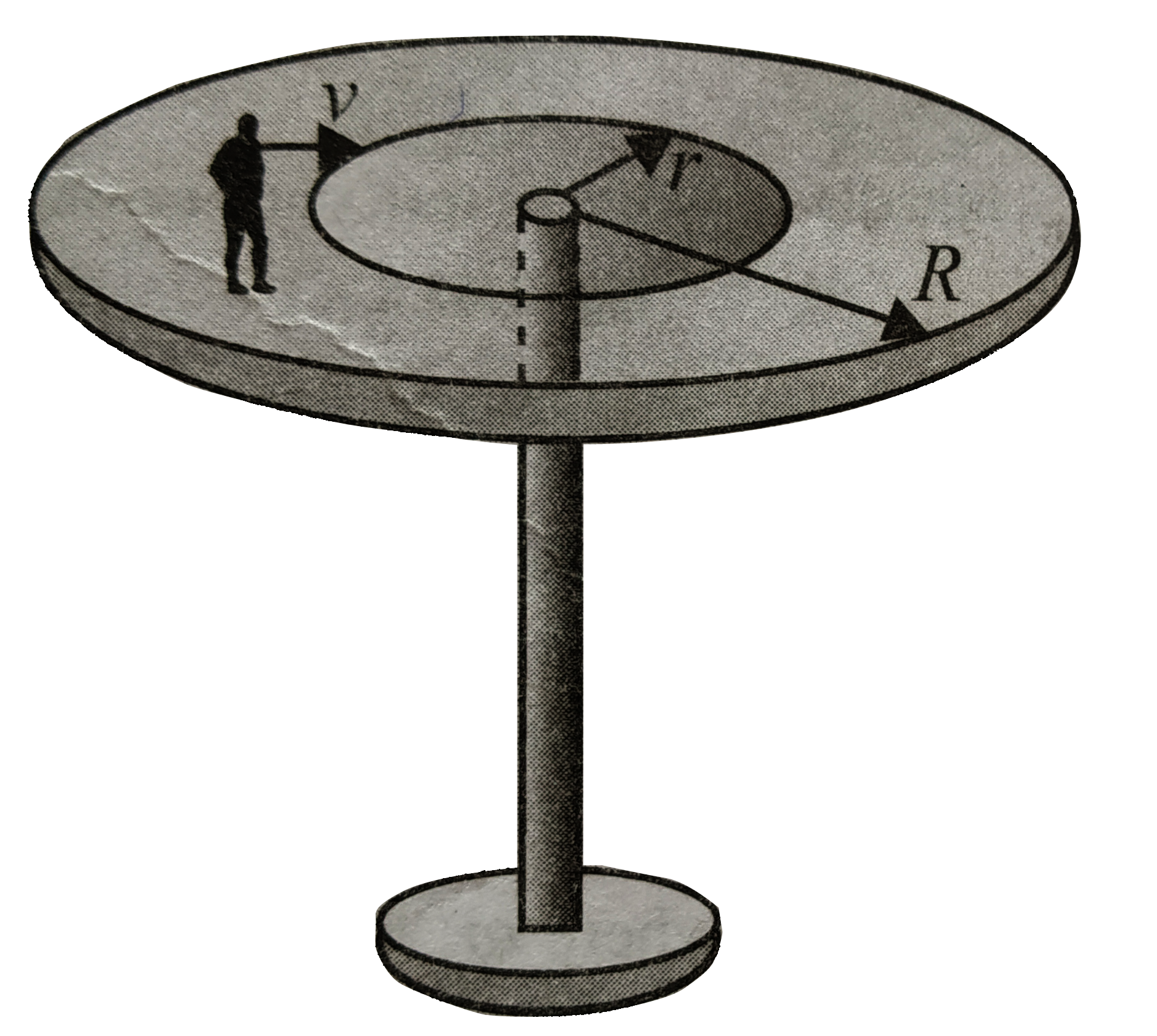
View SolutionA man of mass m stands on a horizontal platform in the shape of a disc of mass m and radius R, pivoted on a vertical axis through its centre about which it can freely rotate. The man starts to move around the centre of the disc in a circle of radius r with a velocity v relative to the disc. Calculate the angular velocity of the disc.
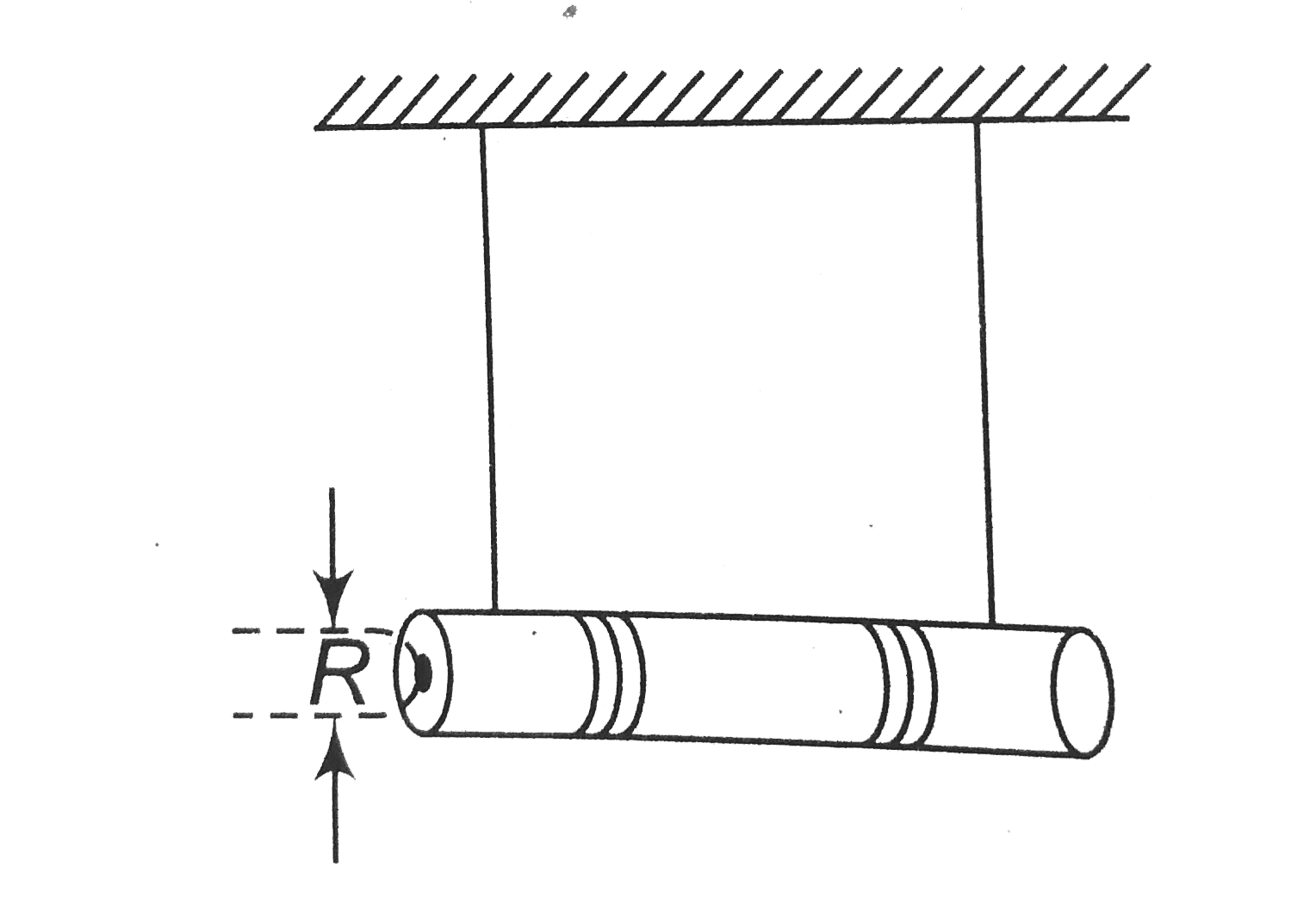
View SolutionA cylindrical rod of mass M, length L and radius R has two cords wound around it whose ends are attached to the ceiling. The rod is held horizontally with the two cords vertical. When the rod is released, the cords unwind and the rod rotates the linear acceleration of the cylinder as it falls, is :
 .
.
View SolutionA cylindrical capacitor with external radius R, internal radius R−d(d<<R), length l and mass M hangs on an insulating cord in a region where there is a homogenous, vertical magnetic field of strength B. It can rotate freely as a whole around its vertical axis, but is constrained, so that it can not move horizontally. The capacitor is charged and there is a voltage difference
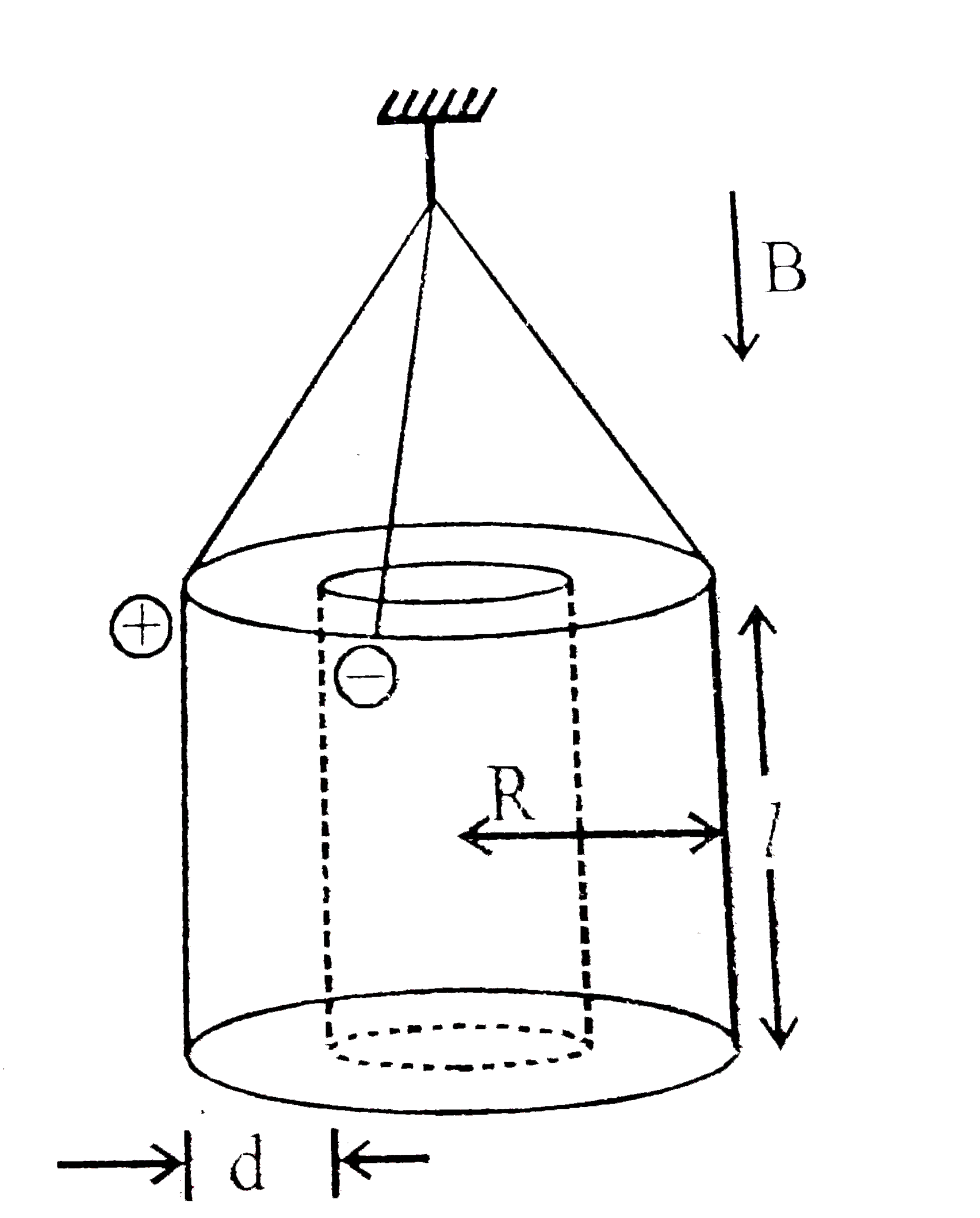
Charge on capacitor is given by
View SolutionA cylindrical capacitor with external radius R, internal radius R-d(dltltR ) , length l and mass M hangs on an insulating cord in a region where there is a homogenous, vertical magnetic field of strength B. It can rotate freely as a whole around its vertical axis, but is constrained, so that it can not move horizontally. The capacitor is charged and there is a voltage difference If without being mechaically disturbed, the capacitor is discharged through an internal radial wire then find maximum angular velocity of capacitor
View Solutionएक ठोस बेलन का द्रव्यमान M त्रिज्या R तथा लम्बाई L है। इसका अपनी अक्ष के परितः जड़त्व आघूर्ण लिखिए।
View Solutionद्रव्यमान M तथा त्रिज्या R की एकसमान डिस्क एक क्षैतिज अक्ष पर स्थित है। एक द्रव्यमान m का पिण्ड द्रव्यमान रहित डोरी जो कि डिस्क की परिधि पर लिपटी हुई है, से ऊर्ध्वाधरतः लटक रहा है। गिरते हुए पिण्ड (m) का त्वरण है :
View SolutionMoment of inertia of a cylindrical shell of mass M, radius R and length L about its geometrical axis would be -
View SolutionA capacitor is made of two circular plates of radius R each, separated by a distance d<<R. The capacitor is connected to a constant voltage. A thin conducting disc of radius r<<R and thickness t<<r is placed at a center of the bottom plate. Find the minimum voltage required to lift the disc if the mass of the disc is m.
View SolutionA cylindrical rod of mass 'm' length L and radius 'R' has two cords wound around it whose ends are attached to a rigid support. The rod is held horozontally with the two cords vertical. When the rod is released, the cords unwind and rod rotates. Find the tension in the cords as they unwound and determine the linear acceleration of the cylinder as it falls.
View SolutionA man of mass m stands on a horizontal platform in the shape of a disc of mass m and radius R, pivoted on a vertical axis thorugh its centre about which it can freely rotate. The man starts to move aroung the centre of the disc in a circle of radius r with a velocity v relative to the disc. Calculate the angular velocity of the disc.

View SolutionMoment of inertia of a cylindrical shell of mass M, radius R and length L about its geometrical axis would be -
View Solution
